题目内容
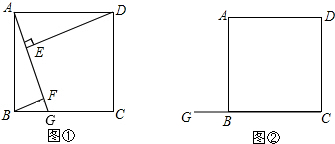
如图①,四边形ABCD是正方形,点G是BC上任意一点,DE⊥AG于点E,BF⊥AG于点F.
(1)求证:DE-BF=EF;
(2)若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明);
(3)若AB=2a,点G为BC边中点时,试探究线段EF与GF之间的数量关系,并通过计算来验证你的结论.
(1)求证:DE-BF=EF;
(2)若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明);
(3)若AB=2a,点G为BC边中点时,试探究线段EF与GF之间的数量关系,并通过计算来验证你的结论.

分析:(1)根据正方形的四条边都相等可得DA=AB,再根据同角的余角相等求出∠BAF=∠ADE,然后利用“角角边”证明△ABF和△DAE全等,再根据全等三角形对应边相等可得BF=AE,AF=DE,然后根据图形列式整理即可得证;
(2)根据题意作出图形,然后根据(1)的结论可得BF=AE,AF=DE,然后结合图形写出结论即可;
(3)根据中点定义求出BG,再利用勾股定理列式求出AG的长,然后利用△ABG的面积列式求出BF的长,再根据勾股定理列式求出FG的长,然后求出AF、AE、BF的长,再表示出EF的长,从而得解.
(2)根据题意作出图形,然后根据(1)的结论可得BF=AE,AF=DE,然后结合图形写出结论即可;
(3)根据中点定义求出BG,再利用勾股定理列式求出AG的长,然后利用△ABG的面积列式求出BF的长,再根据勾股定理列式求出FG的长,然后求出AF、AE、BF的长,再表示出EF的长,从而得解.
解答:(1)证明:∵四边形ABCD是正方形,BF⊥AG,DE⊥AG,
∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
,
∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE,
∴DE-BF=AF-AE=EF;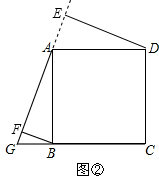
(2)解:如图②,DE+BF=EF;
(3)解:EF=2FG.理由如下:
∵AB=2a,点G为BC边中点,
∴BG=a,
根据勾股定理得,AG=
=
=
a,
又∵AB⊥BC,BF⊥AG,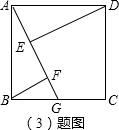
∴S△ABG=
×
a•BF=
•2a•a,
∴BF=
a,
根据勾股定理得,FG=
=
=
a,
∴AF=AG-FG=
a-
a=
a,
∵AE=BF=
a,
∴EF=AG-AE-FG=
a-
a-
a=
a,
∴EF=2FG.
∴DA=AB,∠BAF+∠DAE=∠DAE+∠ADE=90°,
∴∠BAF=∠ADE,
在△ABF和△DAE中,
|
∴△ABF≌△DAE(AAS),
∴BF=AE,AF=DE,
∴DE-BF=AF-AE=EF;

(2)解:如图②,DE+BF=EF;
(3)解:EF=2FG.理由如下:
∵AB=2a,点G为BC边中点,
∴BG=a,
根据勾股定理得,AG=
| AB2+BG2 |
| (2a)2+a2 |
| 5 |
又∵AB⊥BC,BF⊥AG,

∴S△ABG=
| 1 |
| 2 |
| 5 |
| 1 |
| 2 |
∴BF=
2
| ||
| 5 |
根据勾股定理得,FG=
| BG2-BF2 |
a2-(
|
| ||
| 5 |
∴AF=AG-FG=
| 5 |
| ||
| 5 |
4
| ||
| 5 |
∵AE=BF=
2
| ||
| 5 |
∴EF=AG-AE-FG=
| 5 |
2
| ||
| 5 |
| ||
| 5 |
2
| ||
| 5 |
∴EF=2FG.
点评:本题考查了正方形的性质,全等三角形的判定与性质,勾股定理的应用,熟记正方形的四条边都相等,每一个角都是直角,然后求出三角形全等是解题的关键.

练习册系列答案
相关题目
 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.