题目内容
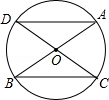
已知:如图,⊙O是△ABC的外接圆,AB为⊙O的直径,弦CD交AB于E,
∠BCD=∠BAC .
(1)求证:AC=AD;
(2)过点C作直线CF,交AB的延长线于点F,若∠BCF=30°,则结论“CF一定是⊙O的切线”是否正确?若正确,请证明;若不正确,请举反例.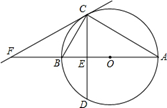
∠BCD=∠BAC .
(1)求证:AC=AD;
(2)过点C作直线CF,交AB的延长线于点F,若∠BCF=30°,则结论“CF一定是⊙O的切线”是否正确?若正确,请证明;若不正确,请举反例.

(1)证明见解析(2)不正确,反例见解析
(1)证明:∵∠BCD=∠BAC,∴弧BC=弧BD。
∵ AB为⊙O的直径,∴AB⊥CD,CE=DE。
∴AC=AD。
(2)解:不正确,如当∠CAB=20°时,CF不是⊙O的切线。
如图, 连接OC。
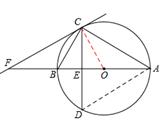
∵ OC=OA,∴∠OCA=20°。
∵∠ACB=90°,∴∠OCB=70°。
又∵∠BCF=30°,∴∠FCO=100°。
∴CO与FC不垂直.。∴此时CF不是⊙O的切线.。
(1)连接AD.根据∠BCD=∠BAC,∠CBE=∠ABC,证出△CBE∽△ABC,可得∠BEC=90°,于是∠D=∠CBA=∠ACD,故AC=AD。
(2)不正确。可令∠CAB=20°,连接OC,据此推出∠OCF≠90°,从而证出∠BCF=30°时“CF不一定是⊙O的切线”
∵ AB为⊙O的直径,∴AB⊥CD,CE=DE。
∴AC=AD。
(2)解:不正确,如当∠CAB=20°时,CF不是⊙O的切线。
如图, 连接OC。

∵ OC=OA,∴∠OCA=20°。
∵∠ACB=90°,∴∠OCB=70°。
又∵∠BCF=30°,∴∠FCO=100°。
∴CO与FC不垂直.。∴此时CF不是⊙O的切线.。
(1)连接AD.根据∠BCD=∠BAC,∠CBE=∠ABC,证出△CBE∽△ABC,可得∠BEC=90°,于是∠D=∠CBA=∠ACD,故AC=AD。
(2)不正确。可令∠CAB=20°,连接OC,据此推出∠OCF≠90°,从而证出∠BCF=30°时“CF不一定是⊙O的切线”

练习册系列答案
相关题目
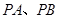 分别与
分别与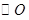 相切于点
相切于点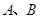 ,点
,点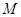 在
在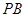 上,且
上,且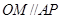 ,
,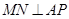 ,垂足为
,垂足为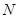 .
.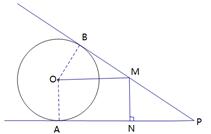
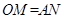 ;
;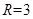 ,
,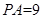 ,求
,求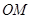 的长
的长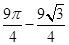 cm2.
cm2.
 cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是_________.
cm,以点A为圆心,以3cm为半径作⊙A,则BC所在直线与⊙A的位置关系是_________.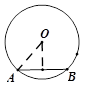
 为圆心的两个同心圆中,大圆的弦
为圆心的两个同心圆中,大圆的弦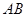 是小圆的切线.若大圆半径为
是小圆的切线.若大圆半径为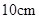 ,小圆半径为
,小圆半径为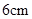 ,则弦
,则弦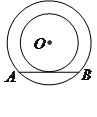
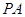 是
是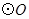 的切线,切点为A,PA=2
的切线,切点为A,PA=2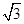 ,∠APO=30°,则
,∠APO=30°,则