Question

【题目】求证：全等三角形对应的角平分线相等。

Answer 1

【答案】证明见详解

【解析】

作出图形，结合图形写出已知、求证，根据全等三角形对应边相等、对应角相等，AB=A′B′，∠B=∠B′，∠BAC=∠B′A′C′，又AD、A′D′是∠BAC和∠B′A′C′的平分线，所以∠BAD=∠B′A′D′，根据角边角判定定理可得△ABD和△A′B′D′全等，所以角平分线AD、A′D′相等．

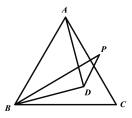
已知：如图，△ABC≌△A′B′C′，AD、A′D′是∠BAC和∠B′A′C′的平分线，

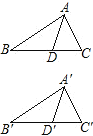
求证：AD=A′D′，

证明：∵△ABC≌△A′B′C′，

∴∠B=∠B′，AB=A′B′，

∠BAC=∠B′A′C′，

∵AD平分∠BAC，A′D′平分∠B′A′C′，

∴∠BAD=∠B′A′D′，

∴△ABD≌△A′B′D′，

∴AD=A′D′．