ћвƒњƒЏ»Ё
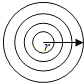
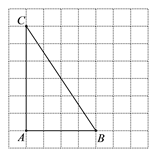
°Њћвƒњ°њ»зЌЉ£ђ‘Џ∆љ√ж÷±љ«„ш±кѕµ÷–£ђ÷±ѕяlќ™’э±»јэЇѓ эy=xµƒЌЉѕу£ђµгA1µƒ„ш±кќ™£®1£ђ0£©£ђєэµгA1„чx÷бµƒієѕяљї÷±ѕяl”ЏµгD1£ђ“‘A1D1ќ™±я„ч’эЈљ–ќA1B1C1D1£їєэµгC1„ч÷±ѕяlµƒієѕя£ђіє„гќ™A2£ђљїx÷б”ЏµгB2£ђ“‘A2B2ќ™±я„ч’эЈљ–ќA2B2C2D2£їєэµгC2„чx÷бµƒієѕя£ђіє„гќ™A3£ђљї÷±ѕяl”ЏµгD3£ђ“‘A3D3ќ™±я„ч’эЈљ–ќA3B3C3D3£ђ°≠£ђ∞ііЋєж¬…≤ў„чѕ¬Ћщµ√µљµƒ’эЈљ–ќAnBnCnDnµƒ√жїэ «_____£Ѓ

°Њір∞Є°њ£®![]() £©n©Б1
£©n©Б1
°Њљвќц°њЄщЊЁ’э±»јэЇѓ эµƒ–‘÷ µ√µљ°ѕD1OA1=45°г£ђЈ÷±р«у≥ц’эЈљ–ќA1B1C1D1µƒ√жїэ°Ґ’эЈљ–ќA2B2C2D2µƒ√жїэ£ђ„№љбєж¬…љвір£Ѓ
°я÷±ѕяlќ™’э±»јэЇѓ эy=xµƒЌЉѕу£ђ
°а°ѕD1OA1=45°г£ђ
°аD1A1=OA1=1£ђ
°а’эЈљ–ќA1B1C1D1µƒ√жїэ=1=£®![]() £©1©Б1£ђ
£©1©Б1£ђ
”…єіє…ґ®јнµ√£ђOD1=![]() £ђD1A2=
£ђD1A2=![]() £ђ
£ђ
°аA2B2=A2O=![]() £ђ
£ђ
°а’эЈљ–ќA2B2C2D2µƒ√жїэ=![]() =£®
=£®![]() £©2©Б1£ђ
£©2©Б1£ђ
Ќђјн£ђA3D3=OA3=![]() £ђ
£ђ
°а’эЈљ–ќA3B3C3D3µƒ√жїэ=![]() =£®
=£®![]() £©3©Б1£ђ
£©3©Б1£ђ
°≠
”…єж¬…њ…÷™£ђ’эЈљ–ќAnBnCnDnµƒ√жїэ=£®![]() £©n©Б1£ђ
£©n©Б1£ђ
є ір∞Єќ™£Ї£®![]() £©n©Б1£Ѓ
£©n©Б1£Ѓ

°Њћвƒњ°њƒ≥єЂЋЊ”ы’–∆Є“ї√ы≤њ√≈Њ≠јн£ђґ‘Љ„°Ґ““°Ґ±ы»э√ыЇт—°»Ћљш––ЅЋ»эѕоЋЎ÷ ≤в ‘£ЃЄчѕо≤в ‘≥…Љ®»з±нЄсЋщ Њ£Ї
≤в ‘ѕоƒњ | ≤в ‘≥…Љ® | ||
Љ„ | ““ | ±ы | |
„®“µ÷™ ґ | 74 | 87 | 90 |
”п—‘ƒ№Ѕ¶ | 58 | 74 | 70 |
„џЇѕЋЎ÷ | 87 | 43 | 50 |
£®1£©»зєыЄщЊЁ»эіќ≤в ‘µƒ∆љЊщ≥…Љ®»Јґ®»Ћ—°£ђƒ«√іЋ≠љЂ±ї¬Љ”√£њ
£®2£©ЄщЊЁ µЉ –и“™£ђєЂЋЊљЂ„®“µ÷™ ґ°Ґ”п—‘ƒ№Ѕ¶ЇЌ„џЇѕЋЎ÷ »эѕо≤в ‘µ√Ј÷∞і4£Ї3£Ї1µƒ±»јэ»Јґ®√њЄц»Ћµƒ≤в ‘„№≥…Љ®£ђіЋ ±Ћ≠љЂ±ї¬Љ”√£њ
£®3£©«л÷Ў–¬…иЉ∆„®“µ÷™ ґ°Ґ”п—‘ƒ№Ѕ¶ЇЌ„џЇѕЋЎ÷ »эѕо≤в ‘µ√Ј÷µƒ±»јэјі»Јґ®√њЄц»Ћµƒ≤в ‘„№≥…Љ®£ђ єµ√““±ї¬Љ”√£ђ»ф÷Ў–¬…иЉ∆µƒ±»јэќ™x£Їy£Ї1£ђ«“x+y+1£љ10£ђ‘тx£љ°° °°£ђy£љ°° °°£Ѓ£®–і≥цx”лyµƒ“ї„й’ы э÷µЉіњ…£©£Ѓ
°Њћвƒњ°њќ™ЅЋЅЋљвƒ≥–£—І…ъµƒ…нЄя«йњц£ђЋжїъ≥й»°Є√–£ƒ–…ъ°Ґ≈Ѓ…ъљш––≥й—щµч≤й£ђ“—÷™≥й»°µƒ—щ±Њ÷–£ђƒ–…ъ°Ґ≈Ѓ…ъµƒ»Ћ эѕаЌђ£ђјы”√Ћщµ√ эЊЁїж÷∆»зѕ¬Ќ≥Љ∆ЌЉ±н£Ї
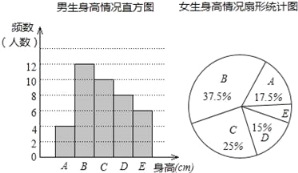
…нЄя«йњцЈ÷„й±н£®µ•ќї£Їcm£©
„й±р | …нЄя |
A | x£Љ160 |
B | 160°№x£Љ165 |
C | 165°№x£Љ170 |
D | 170°№x£Љ175 |
E | x°Ё175 |
ЄщЊЁЌЉ±нћбє©µƒ–≈ѕҐ£ђїЎірѕ¬Ѕ–ќ ћв£Ї
£®1£©—щ±Њ÷–£ђƒ–…ъµƒ…нЄя÷Џ э‘Џ°° °°„й£ђ÷–ќї э‘Џ°° °°„й£ї
£®2£©—щ±Њ÷–£ђ≈Ѓ…ъ…нЄя‘ЏE„йµƒ»Ћ э”–°° °°»Ћ£ї
£®3£©“—÷™Є√–£є≤”–ƒ–…ъ600»Ћ£ђ≈Ѓ…ъ480»Ћ£ђ«лєјЉ∆…нЄя‘Џ165°№x£Љ175÷ЃЉдµƒ—І…ъ‘Љ”–ґа…ў»Ћ£њ