题目内容
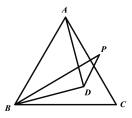
【题目】如图,D为等边△ABC内的一点,AD=BD,BP=AB,∠DBP=∠DAC,若∠DBC=15°,则∠ADP的度数是__________
【答案】45°
【解析】
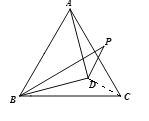
如图,连接CD,已知△ABC是等边三角形,则AB=AC=BC,又AD=BD,易证△BDC≌△ADC,可得∠DCB=∠DCA=30°,∠DBC=∠DAC,已知∠DAC=∠DBP,又已知BP=BA,可得BP=AC,所以△DBP≌△DAC,所以∠P=∠ACD=30°,再证明三角形ABD是等腰直角三角形,得到∠ADB=90°,利用三角形的内角和求出∠ADP的度数.
解:如图,连接CD,
∵△ABC是等边三角形,
∴AB=AC=BC,又AD=BD,DC是公共边,
∴△BDC≌△ADC(SSS),
∴∠DCB=∠DCA=![]() ×60°=30°,∠DBC=∠DAC,
×60°=30°,∠DBC=∠DAC,
∵∠DAC=∠DBP,
又已知BP=BA,
∴BP=AC,
∵AD=BD,
∴△DBP≌△DAC(SAS),
∴∠P=∠ACD=30°.
∵∠DBC=15°,∴∠DBP=15°,∠ABD=45°,
又AD=BD,∴△ABD是等腰直角三角形,
∴∠ADB=90°,
故∠ADP=180°-∠DBP-∠P-∠ADB=45°,
故填:45°.

【题目】近期电影《少年的你》受到广大青少年的喜爱,某校七年级1班2班的几名同学请他们的家长在网上买票,家长了解到某电影院的活动,设购买电影票的张数为![]()
购买张数 |
|
|
|
每张票的价格 |
|
|
|
家长沟通后决定两个班的同学在期中考试结束后去观看。两个班共有![]() 人,期中
人,期中![]() 班人数多于
班人数多于![]() 不足
不足![]() 人。经过估算,如果两个班都以班为单位购买,则一共应付
人。经过估算,如果两个班都以班为单位购买,则一共应付![]() 元。
元。
![]() 求两个班有多少个同学?
求两个班有多少个同学?
![]() 如果两个班联合起来,作为一个团体购票,可以节省多少钱?
如果两个班联合起来,作为一个团体购票,可以节省多少钱?
![]() 如果七年级
如果七年级![]() 班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?
班同学作为一个团体购票,你认为如何购票才最省钱?可以节省多少钱?