题目内容
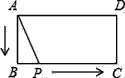
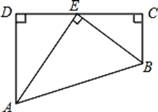
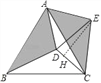
【题目】如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E.
(1)DE=_____;
(2)∠CDE的正切值为_____.

【答案】 5, 3![]()
【解析】分析:(1)先利用等边三角形的性质AB=AC,∠BAC=60°,再根据旋转的性质得AD=AE, ∠DAE=∠BAC=60°,CE=BD=6,然后判断△ADE为等边三角形得到DE的长;(2) 作EH⊥CD于H, 设DH=x,则CH=4﹣x,利用勾股定理得到52﹣x2=62﹣(4-x),解得x=![]() ,再计算出EH的长,然后利用正切的定义求解.
,再计算出EH的长,然后利用正切的定义求解.
详解:(1)∵△ABC为等边三角形,
∴AB=AC,∠BAC=60°,
∵△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,
∴AD=AE,∠DAE=∠BAC=60°,CE=BD=6,
∴△ADE为等边三角形,
∴DE=AD=5;
(2)作EH⊥CD于H,如图,
设DH=x,则CH=4﹣x,
在Rt△EDH中,EH2=DE2﹣DH2=52﹣x2,
在Rt△ECH中,EH2=CE2﹣CH2=62﹣(4﹣x)2,
∴52﹣x2=62﹣(4﹣x)2,解得x=![]() ,
,
∴EH=![]() =
=![]() ,
,
∴tan∠EDH=![]() =3
=3![]() ,
,
即∠CDE的正切值为3![]() .
.
故答案为5,3![]() .
.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目