题目内容
【题目】如图,四边形ABCD中,∠D=∠C=90°,点E在CD上,AE平分∠DAB,BE平分∠CBA,若AD=4,AB=6,求CB的长。
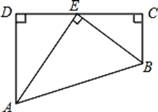
【答案】2.
【解析】
过点E作EF⊥AB于点F,根据角平分线的性质可知DE=EF,EF=CE,根据AAS定理可得△ADE≌△AFE,故AD=AF=4,求出BF的长,同理可得△BCE≌△BFE,故可得出BC=BF,由此得出结论.
解:过点E作EF⊥AB于点F,

∵AE平分∠DAB,BE平分∠CBA,
∴∠DAE=∠FAE,∠CBE=∠FBE,
在△ADE与△AEF中,
 ,
,
∴△ADE≌△AFE(AAS),
∴AD=AF=4,
∴BF=AB﹣AF=6﹣4=2.
同理可得△BCE≌△BFE,
∴BC=BF=2.

练习册系列答案
相关题目