题目内容
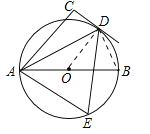
【题目】如图所示,AB为⊙O的直径,AD平分∠CAB,AC⊥CD,垂足为C.
(1)判断CD与⊙O的位置关系,并说明理由;
(2)求证:∠CDA=∠AED.

【答案】(1)证明见解析;(2)见解析
【解析】试题分析:(1)连接OD,根据OA=OD,推出∠OAD=∠CAD,求出∠ODA=∠CAD,求出OD⊥CD,根据切线的判定推出即可;
(2)连接BD,利用AB为直径的性质进行解答.
试题解析:证明:(1)CD是⊙O的切线.证明如下:
连接OD.∵OA=OD,∴∠ODA=∠OAD.∵AD平分∠CAB,∴∠OAD=∠CAD,∴∠ODA=∠CAD.∵AC⊥CD,即∠CAD+∠CDA=90°,∴∠ODA+∠CDA=90°,∴OD⊥CD,即CD是⊙O的切线;
(2)连接BD.∵AB为直径,∴∠ADB=90°,∴∠B+∠BAD=90°,∠B=∠AED,∴∠AED+∠BAD=90°.∵∠CDA+∠CAD=90°,∠CAD=∠BAD,∴∠CDA=∠AED.

练习册系列答案
相关题目