��Ŀ����
����Ŀ����ͼ����֪������y=![]() x2+3x��8��ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��
x2+3x��8��ͼ����x�ύ��A��B���㣨��A�ڵ�B���Ҳࣩ����y�ύ�ڵ�C��
��1����ֱ��BC�Ľ���ʽ��
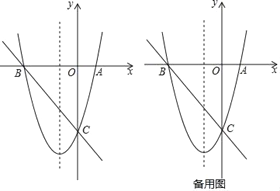
��2����F��ֱ��BC�·��������ϵ�һ�㣬����BCF��������ʱ���������ߵĶԳ�������һ��P��ʹ����BFP���ܳ���С���������F������͵�P�����ꣻ
��3���ڣ�2���������£��Ƿ���������ĵ�Q��0��m����ʹ����BFQΪ���������Σ�����У���ֱ��д����Q�����ꣻ���û�У���˵�����ɣ�
���𰸡���1��y=��x��8����2��F����4����12����P����3����10������3��������.
�������������������1�����ô���ϵ�������B��C�������꼴�ɽ��������
��2����ͼ1������FN��y�ύBC��N����F��m�� ![]() m2+3m��8������N��m����m��8�����������κ��������ö��κ��������������F��������Ϊ��B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С�����ֱ��AF�Ľ���ʽ���ɽ��������
m2+3m��8������N��m����m��8�����������κ��������ö��κ��������������F��������Ϊ��B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С�����ֱ��AF�Ľ���ʽ���ɽ��������
��3����ͼ2������������������������FQ1=FBʱ��Q1��0��0��������BF=BQʱ����֪Q2��0���� ![]() ����Q3��0��
����Q3��0�� ![]() ��������Q4B=Q4Fʱ����Q��0��m�����������̼��ɽ��������
��������Q4B=Q4Fʱ����Q��0��m�����������̼��ɽ��������
���������������1������������y=![]() x2+3x��8����y=0���õ���
x2+3x��8����y=0���õ��� ![]() x2+3x��8=0�������x=��8��2����B����8��0����A��2��0������x=0���õ���y=��8����A��2��0����B����8��0����C��0����8������ֱ��BC�Ľ���ʽΪy=kx+b��������
x2+3x��8=0�������x=��8��2����B����8��0����A��2��0������x=0���õ���y=��8����A��2��0����B����8��0����C��0����8������ֱ��BC�Ľ���ʽΪy=kx+b�������� ![]() �������
������� ![]() ����ֱ��BC�Ľ���ʽΪy=��x��8��
����ֱ��BC�Ľ���ʽΪy=��x��8��
��2����ͼ1������FN��y�ύBC��N����F��m�� ![]() m2+3m��8������N��m����m��8��
m2+3m��8������N��m����m��8��
��S��FBC=S��FNB+S��FNC=![]() FN��8=4FN=4[����m��8������
FN��8=4FN=4[����m��8������![]() m2+3m��8��]=��2m2��16m=��2��m+4��2+32������m=��4ʱ����FBC����������ֵ����ʱF����4����12�����������ߵĶԳ���x=��3����B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С����ֱ��AF�Ľ���ʽΪy=ax+b��������
m2+3m��8��]=��2m2��16m=��2��m+4��2+32������m=��4ʱ����FBC����������ֵ����ʱF����4����12�����������ߵĶԳ���x=��3����B���ڶԳ���ĶԳƵ���A������AF���Գ�����P����ʱ��BFP���ܳ���С����ֱ��AF�Ľ���ʽΪy=ax+b�������� ![]() �������
������� ![]() ����ֱ��AF�Ľ���ʽΪy=2x��4����P����3����10��������F������͵�P������ֱ���F����4����12����P����3����10����
����ֱ��AF�Ľ���ʽΪy=2x��4����P����3����10��������F������͵�P������ֱ���F����4����12����P����3����10����
��3����ͼ2�У���B����8��0����F����4��0������BF=![]() =
=![]() �����������������
�����������������
����FQ1=FBʱ��Q1��0��0����
����BF=BQʱ����֪Q2��0���� ![]() ����Q3��0��
����Q3��0�� ![]() ����
����
����Q4B=Q4Fʱ����Q4��0��m��������82+m2=42+��m+12��2�����m=��4����Q4��0����4��
��Q��������0��0����0�� ![]() ����0����
����0����![]() ����0����4����
����0����4����

����Ŀ��ij��6��ͬѧ������(��λ��cm)������±���
ͬѧ | A | B | C | D | E | F |
���� | 165 | 166 | 171 | |||
������༶ƽ�����ߵIJ�ֵ | ��1 | ��2 | ��3 | ��3 |
(1)��ɱ��пհIJ��֣�
(2)���ǵ��������������������٣�
(3)����6�˵�ƽ�������Ƕ��٣�








