题目内容
【题目】如图,方格中,每个小正方形的边长都是单位1,△ABC在平面直角坐标系中的位置如图.
(1)画出将△ABC向右平移2个单位得到△A1B1C1;
(2)画出将△ABC绕点O顺时针方向旋转90°得到的△A2B2C2;
(3)求△A1B1C1与△A2B2C2重合部分的面积.
【答案】
(1)
如图,△A1B1C1为所作

(2)
如图,△A2B2C2为所作

(3)
解:B2C2与A1B1相交于点E,B2A2与A1B1相交于点F,如图,
∵B2(0,1),C2(2,3),B1(1,0),A1(2,5),A2(5,0),
∴直线A1B1为y=5x﹣5,
直线B2C2为y=x+1,
直线A2B2为y=﹣ ![]() x+1,
x+1,
由 ![]() 解得
解得 ![]() ,∴点E(
,∴点E( ![]() ,
, ![]() ),
),
由 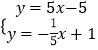 解得
解得 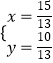 ,∴点F(
,∴点F( ![]() ,
, ![]() ).
).
∴S△BEF= ![]() ×
× ![]() ﹣
﹣ ![]()
![]()
![]() ﹣
﹣ ![]()
![]()
![]() ﹣
﹣ ![]()
![]()
![]() =
= ![]() .
.
∴△A1B1C1与△A2B2C2重合部分的面积为 ![]()
【解析】(1)将△ABC向右平移2个单位即可得到△A1B1C1 . (2)将△ABC绕点O顺时针方向旋转90°即可得到的△A2B2C2 . (3)B2C2与A1B1相交于点E,B2A2与A1B1相交于点F,如图,求出直线A1B1 , B2C2 , A2B2 , 列出方程组求出点E、F坐标即可解决问题.本题考查了作图﹣旋转变换:根据旋转的性质可知,对应角都相等都等于旋转角,对应线段也相等,由此可以通过作相等的角,在角的边上截取相等的线段的方法,找到对应点,顺次连接得出旋转后的图形.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目






