题目内容
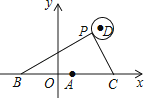
【题目】如图，是一圆锥的左视图，根据图中所标数据，圆锥侧面展开图的扇形圆心角的大小为（ ） 
A.90°
B.120°
C.135°
D.150°
【答案】B
【解析】解：∵圆锥的底面半径为3，
∴圆锥的底面周长为6π，
∵圆锥的高是6 
，∴圆锥的母线长为 
=9，
设扇形的圆心角为n°，
∴ 
=6π，
解得n=120．
答：圆锥的侧面展开图中扇形的圆心角为120°．
故选B．
根据圆锥的底面半径得到圆锥的底面周长，也就是圆锥的侧面展开图的弧长，根据勾股定理得到圆锥的母线长，利用弧长公式可求得圆锥的侧面展开图中扇形的圆心角．本题考查了圆锥的计算，圆锥的侧面展开图是一个扇形，此扇形的弧长等于圆锥底面周长，扇形的半径等于圆锥的母线长．本题就是把的扇形的弧长等于圆锥底面周长作为相等关系，列方程求解．
练习册系列答案
相关题目
