题目内容
【题目】已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．
（1）求证：BD=CE；
（2）求证：∠M=∠N．
【答案】
（1）
证明：在△ABD和△ACE中，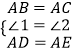 
，
∴△ABD≌△ACE（SAS），
∴BD=CE；
（2）
证明：∵∠1=∠2，
∴∠1+∠DAE=∠2+∠DAE，
即∠BAN=∠CAM，
由（1）得：△ABD≌△ACE，
∴∠B=∠C，
在△ACM和△ABN中，
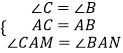
∴△ACM≌△ABN（ASA），
∴∠M=∠N．
【解析】（1）由SAS证明△ABD≌△ACE，得出对应边相等即可（2）证出∠BAN=∠CAM，由全等三角形的性质得出∠B=∠C，由AAS证明△ACM≌△ABN，得出对应角相等即可．本题考查了全等三角形的判定与性质；证明三角形全等是解决问题的关键．
练习册系列答案
课堂全解字词句段篇章系列答案
相关题目
