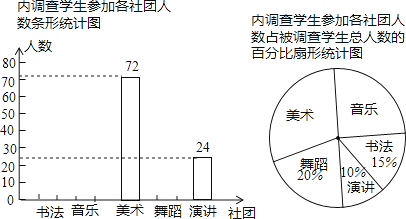
��Ŀ����
����Ŀ����֪��ABC�ǵ���ֱ�������Σ���BAC=90�㣬CD= ![]() BC��DE��CE��DE=CE������AE����M��AE���е㣮
BC��DE��CE��DE=CE������AE����M��AE���е㣮 
��1����ͼ1������D��BC���ϣ�����CM����AB=4ʱ����CM�ij���
��2����ͼ2������D�ڡ�ABC���ڲ�������BD����N��BD�е㣬����MN��NE����֤��MN��AE��
��3����ͼ3����ͼ2�еġ�CDE�Ƶ�C��ʱ����ת��ʹ��BCD=30�㣬����BD����N��BD�е㣬����MN��̽�� ![]() ��ֵ��ֱ��д�������
��ֵ��ֱ��д�������
���𰸡�
��1��
�⣺��ͼ1�У�
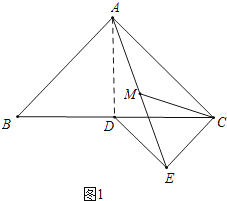
����AD��
��AB=AC=4����BAC=90�㣬
���B=��ACD=45�㣬BC= ![]() =4
=4 ![]() ��
��
��DC= ![]() BC=2
BC=2 ![]() ��
��
��ED=EC����DEC=90�㣬
��DE=EC=2����DCE=��EDC=45�㣬
���ACE=90�㣬
��RT��ACE��AE= ![]() =
= ![]() =2
=2 ![]() ��
��
��AM=ME��
��CM= ![]() AE=
AE= ![]()
��2��
֤������ͼ2�У�

�ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�ED��AB��F��
�ڡ�AMG�͡�EMD�У�
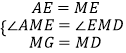 ��
��
���AMG�ա�EMD��
��AG=DE=EC��
��MAG=��MED��
��EF��AG��
���BAG=��BFE=180�㩁��FBC����90�㩁��ECB��=45��+��BCE=��ACE��
�ڡ�ABG�͡�CAE�У�
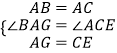 ��
��
���ABG�ա�CAE��
���ABG=��CAE��
�ߡ�CAE+��BAE=90�㣬
���ABG+��BAE=90�㣬
���AOB=90�㣬
��BG��AE��
��DN=NB��DM=MG��
��MN��BG��
��MN��AE
��3��
�⣺��ͼ3�У�
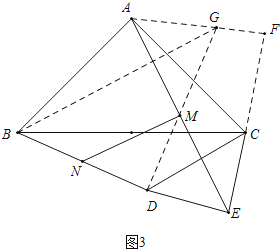
�ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�AG��EC���ڵ�F��
�ߡ�AMG�ա�EMD��
��AG=DE=EC����GAM=��DEM��
��AG��DE��
���F=��DEC=90�㣬
�ߡ�FAC+��ACF=90�㣬��BCD+��ACF=90�㣬��BCD=30�㣬
���BAG=��ACE=120�㣬
�ڡ�ABG�͡�CAE�У�
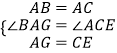 ��
��
���ABG�ա�CAE��
��BG=AE��
��BN=ND��DM=MG��
��BG=AE=2MN��
���FAC=��BCD=30�㣬��BC=2a����CD=a��DE=EC= ![]() a��AC=
a��AC= ![]() a��CF=
a��CF= ![]() a��AF=
a��AF= ![]() a��EF=
a��EF= ![]() a��
a��
��AE= ![]() =
= ![]() a��
a��
��MN= ![]() a��
a��
�� ![]() =
= ![]() =
= ![]()
����������1����֤����ACE��ֱ�������Σ�����CM= ![]() AE�����AE���ɽ�����⣮��2����ͼ2�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�ED��AB��F����֤����AMG�ա�EMD���Ƴ�EF��AG����֤����ABG�ա�CAE���á�ABG=��CAE���ɴ˼��ɽ�����⣮��3����ͼ3�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�AG��EC���ڵ�F����֤����ABG�ա�CAE���õ�BG=AE����BC=2a����RT��AEF�����AE��������λ�߶���MN=
AE�����AE���ɽ�����⣮��2����ͼ2�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�ED��AB��F����֤����AMG�ա�EMD���Ƴ�EF��AG����֤����ABG�ա�CAE���á�ABG=��CAE���ɴ˼��ɽ�����⣮��3����ͼ3�У��ӳ�DM��Gʹ��MG=MD������AG��BG���ӳ�AG��EC���ڵ�F����֤����ABG�ա�CAE���õ�BG=AE����BC=2a����RT��AEF�����AE��������λ�߶���MN= ![]() BG=
BG= ![]() AE���ɴ˼��ɽ�����⣮���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������Ӹ����ߣ�����ȫ�������Σ�ѧ�����Ӹ����ߵķ����������п�ѹ���⣮
AE���ɴ˼��ɽ�����⣮���⿼���������ۺ��⡢ȫ�������ε��ж������ʡ����������ε��ж������ʡ����ɶ�����֪ʶ������Ĺؼ������Ӹ����ߣ�����ȫ�������Σ�ѧ�����Ӹ����ߵķ����������п�ѹ���⣮
�����㾫�������չ��ɶ����ĸ�������������ε��ж��������ǽ����ĸ�������Ҫ֪��ֱ����������ֱ�DZ�a��b��ƽ���͵���б��c��ƽ��,��;a2+b2=c2�����������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ����

 Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д� �����ÿ�ʱѵ��ϵ�д�
�����ÿ�ʱѵ��ϵ�д�