Question

【题目】将线段AB绕点A逆时针旋转60°得到线段AC，继续旋转(0°＜＜120°)得到线段AD，连接CD.

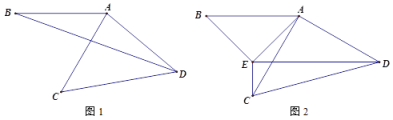
(1)连接BD，如图1，若＝80°，则∠BDC的度数为 ；(直接写出结果)

(2)如图2，以AB为斜边作直角三角形ABE，使得∠B＝∠ACD，连接CE，DE.若∠CED＝90°，求的值.

Answer 1

【答案】（1）30°；（2）90°.

【解析】

（1）根据图形旋转的性质可知AB=AC=AD，再由圆周角定理即可得出结论；

（2）过点AM⊥CD于点M，连接EM，先根据AAS定理得出△AEB≌△AMC，故可得出AE=AM，∠BAE=∠CAM，所以△AEM是等边三角形．根据AC=AD，AM⊥CD可知CM=DM．故可得出点A、C、D在以M为圆心，MC为半径的圆上．由圆周角定理可得出结论．

解：（1）∵线段AC，AD由AB旋转而成，
∴AB=AC=AD．
∴点B、C、D在以A为圆心，AB为半径的圆上．
∴∠BDC=∠BAC=30°．
故答案为：30°；

（2）过点AM⊥CD于点M，连接EM．

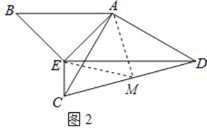
则∠AMD=∠AMC=90°．
在△AEB与△AMC中，
，
∴△AEB≌△AMC（AAS）．
∴AE=AM，∠BAE=∠CAM．
∴∠EAM=∠EAC+∠CAM=∠EAC+∠BAE=∠BAC=60°．
∴△AEM是等边三角形．
∴EM=AM=AE．
∵AC=AD，AM⊥CD，
∴CM=DM．
又∵∠DEC=90°，
∴EM=CM=DM．
∴AM=CM=DM．
∴点A、C、D在以M为圆心，MC为半径的圆上．
∴=∠CAD=90°．