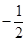题目内容
已知∠ABC=90°,点P为射线BC上任意一点(点P与点B不重合),分别以AB、AP为边在∠ABC的内部作等边△ABE和△APQ,连结QE并延长交BP于点F.
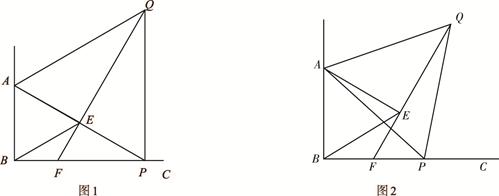
(1)如图1,若AB=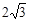 ,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);
,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);
(2)如图2,当点P为射线BC上任意一点时,猜想EF与图中的哪条线段相等(不能添加辅助线产生新的线段),并加以证明;
(3)若AB=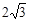 ,设BP=4,求QF的长.
,设BP=4,求QF的长.

(1)如图1,若AB=
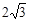 ,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);
,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);(2)如图2,当点P为射线BC上任意一点时,猜想EF与图中的哪条线段相等(不能添加辅助线产生新的线段),并加以证明;
(3)若AB=
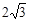 ,设BP=4,求QF的长.
,设BP=4,求QF的长.1)EF=2(2)EF=BF,见解析(3)6
解:(1)EF=2. 3分
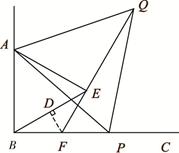
(2)EF=BF. 4分
证明: ∵ ∠BAP=∠BAE-∠EAP=60°-∠EAP,
∠EAQ=∠QAP-∠EAP=60°-∠EAP,
∴ ∠BAP="∠EAQ" .
在△ABP和△AEQ中,
AB=AE,∠BAP=∠EAQ, AP=AQ,
∴ △ABP≌△AEQ.
∴ ∠AEQ=∠ABP=90°.
∴ ∠BEF .
.
又∵ ∠EBF=90°-60°=30°,
∴EF=BF. 8分
(3) 在图1中,过点F作FD⊥BE于点D.
∵ △ABE是等边三角形,
∴ BE=AB=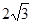 .
.
由(2)得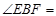 30°,
30°,
在Rt△BDF中, .
.
∴ BF=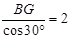 .
.
∴ EF=2 . 10分
∵ △ABP≌△AEQ ,
∴ QE=BP=4. 12分
∴ QF=QE+EF=4+2=6
(1)利用解直角三角形求解
(2)利用全等三角形求证
(3)过点F作FD⊥BE于点D,利用三角函数求出EF的长,再求证△ABP≌△AEQ,求得QE的长,从而求出QF的长

(2)EF=BF. 4分
证明: ∵ ∠BAP=∠BAE-∠EAP=60°-∠EAP,
∠EAQ=∠QAP-∠EAP=60°-∠EAP,
∴ ∠BAP="∠EAQ" .
在△ABP和△AEQ中,
AB=AE,∠BAP=∠EAQ, AP=AQ,
∴ △ABP≌△AEQ.
∴ ∠AEQ=∠ABP=90°.
∴ ∠BEF
 .
.又∵ ∠EBF=90°-60°=30°,
∴EF=BF. 8分
(3) 在图1中,过点F作FD⊥BE于点D.
∵ △ABE是等边三角形,
∴ BE=AB=
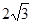 .
.由(2)得
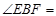 30°,
30°,在Rt△BDF中,
 .
. ∴ BF=
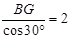 .
. ∴ EF=2 . 10分
∵ △ABP≌△AEQ ,
∴ QE=BP=4. 12分
∴ QF=QE+EF=4+2=6
(1)利用解直角三角形求解
(2)利用全等三角形求证
(3)过点F作FD⊥BE于点D,利用三角函数求出EF的长,再求证△ABP≌△AEQ,求得QE的长,从而求出QF的长

练习册系列答案
相关题目
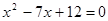 的两根,则这个三角形的斜边长是( )
的两根,则这个三角形的斜边长是( )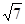

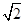 =1.414,
=1.414,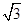 ≈1.732,
≈1.732,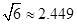 )
)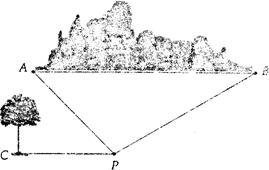
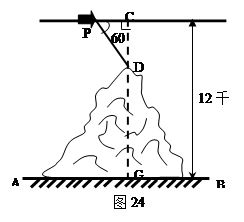
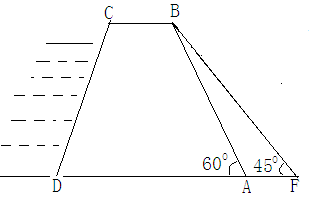
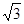 m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=450,求AF的长度(结果精确到1米,参考数据,
m,为加强水坝强度,将坝底从A处向后水平延伸到F处,使新的背水坡的坡角∠F=450,求AF的长度(结果精确到1米,参考数据,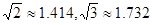 )
)
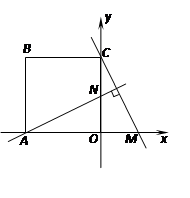
 ,
, ,
,
 ,
, ,
,
 为锐角时有
为锐角时有 ,由此可知:
,由此可知: ( )
( )