题目内容
如图5,一架飞机在空中P处探测到某高山山顶D处的俯角为60°,
此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)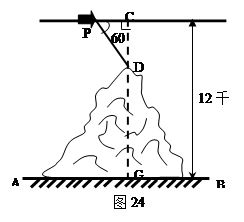
此后飞机以300米/秒的速度沿平行于地面AB的方向匀速飞行,飞行10秒到山顶D的正上方C处,此时测得飞机距地平面的垂直高度为12千米,求这座山的高(精确到0.1千米)

解:延长CD交AB于G,则CG=12(千米)
依题意:PC=300×10=3000(米)=3(千米)
在Rt△PCD中:
PC=3,∠P=60°
CD=PC·tan∠P
=3×tan60°
=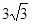
∴12-CD=12-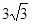 ≈6.8(千米)
≈6.8(千米)
答:这座山的高约为6.8千米.
依题意:PC=300×10=3000(米)=3(千米)
在Rt△PCD中:
PC=3,∠P=60°
CD=PC·tan∠P
=3×tan60°
=
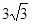
∴12-CD=12-
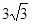 ≈6.8(千米)
≈6.8(千米)答:这座山的高约为6.8千米.
直角三角形中三角函数的计算。

练习册系列答案
相关题目
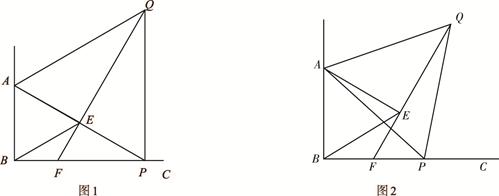
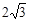 ,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);
,点A、E、P恰好在一条直线上时,求此时EF的长(直接写出结果);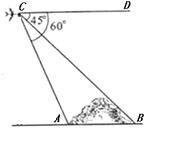
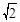 ≈1.4,
≈1.4,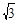 ≈1.7,结果保留整数。)
≈1.7,结果保留整数。)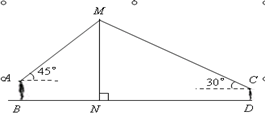
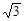 ,过直角顶点C作
,过直角顶点C作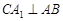 ,垂足为
,垂足为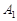 ,再过
,再过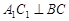 ,垂足为
,垂足为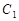 ;过
;过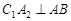 ,垂足为
,垂足为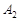 ,再过
,再过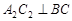 ,垂足为
,垂足为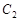 ;……,这样一直做下去,得到一组线段
;……,这样一直做下去,得到一组线段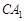 ,
,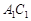 ,
, ,……,则第12条线段
,……,则第12条线段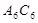 =_
=_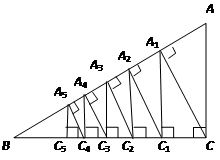
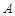 处测得电视塔尖点
处测得电视塔尖点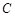 的仰角为
的仰角为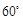 ,沿山坡向上走到
,沿山坡向上走到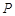 处再测得点
处再测得点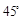 ,已知
,已知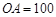 米,山坡坡度
米,山坡坡度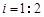 且O 、A、B在同一条直线上.求电视塔
且O 、A、B在同一条直线上.求电视塔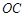 的高度以及此人所在位置点
的高度以及此人所在位置点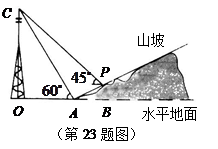
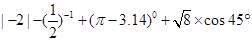 .
.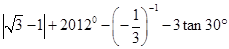 .
.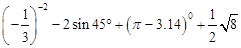 .
.