题目内容
如图，将边长为6的正方形ABCO放置在直角坐标系中，使点A在x轴负半轴上，点C在y轴正半轴上。点M（t，0）在x轴上运动，过A作直线MC的垂线交y轴于点N．
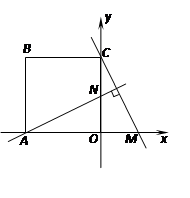
(1) 当t = 2时，tan∠NAO = ▲ ；
(2) 在直角坐标系中，取定点P（3，8），则在点M运动过程中，当以M、N、C、P为顶点的四
边形是梯形时，点M的坐标为 ▲ ．
(1) 当t = 2时，tan∠NAO = ▲ ；
(2) 在直角坐标系中，取定点P（3，8），则在点M运动过程中，当以M、N、C、P为顶点的四
边形是梯形时，点M的坐标为 ▲ ．
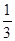、 （3，0）或（4+
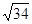，0）或（4-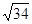，0）(1) 因为ABCO是正方形，AN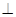
MC,所以∠NAO+∠M=
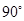,∠M+∠OCM =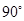,所以∠NAO=∠OCM，即tan∠NAO=tan∠OCM=
=
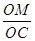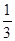
(2) 因为直角坐标系中，取定点P（3，8），则在点M运动过程中，当以M、N、C、P为顶点的四
边形是梯形时，由于A(-6,0)C(0,6)M（x,0）,那么梯形的情况，可能是MN//CP,或者CN//MP,由此可以解得点M的坐标为（3，0）或（4+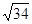，0）或（4-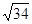，0）
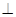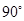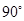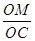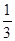
MC,所以∠NAO+∠M=,∠M+∠OCM =,所以∠NAO=∠OCM，即tan∠NAO=tan∠OCM==(2) 因为直角坐标系中，取定点P（3，8），则在点M运动过程中，当以M、N、C、P为顶点的四
边形是梯形时，由于A(-6,0)C(0,6)M（x,0）,那么梯形的情况，可能是MN//CP,或者CN//MP,由此可以解得点M的坐标为（3，0）或（4+
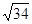，0）或（4-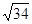，0）
练习册系列答案
名校课堂系列答案
相关题目
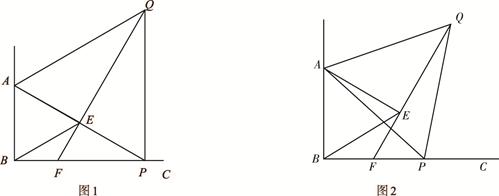
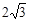，点A、E、P恰好在一条直线上时，求此时EF的长（直接写出结果）；
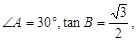AC=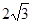
，则AB等于( ) 
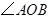如右图放置，则sin∠AOB的值为( ▲ )
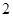
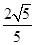
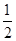
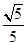
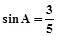, 那么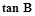
的值等于_____．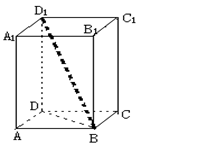
.
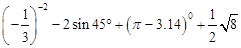