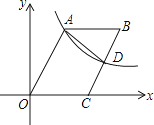��Ŀ����
����Ŀ����ͼ����֪������y=-![]() x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���
x2+bx+c��������ֱ��ڵ�A��0��8����B��8��0���͵�E������C��ԭ��O��ʼ��OA������ÿ��1����λ�����ƶ�������D�ӵ�B��ʼ��BO������ÿ��1����λ�����ƶ�������C��Dͬʱ������������D����ԭ��Oʱ����C��Dֹͣ�˶���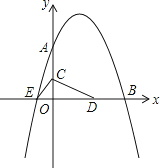
��1��ֱ��д�������ߵĽ���ʽ�� ��
��2�����CED�����S��D���˶�ʱ��t�ĺ�������ʽ����tΪ��ֵʱ����CED���������������Ƕ��٣�
��3������CED��������ʱ�������������Ƿ���ڵ�P����E���⣩��ʹ��PCD��������ڡ�CED���������������ڣ����P������ꣻ�������ڣ���˵�����ɣ�
���𰸡�
��1��y=-![]() x2+3x+8
x2+3x+8
��2��
�⣺�ߵ�A��0��8����B��8��0����
��OA=8��OB=8��
��y=0���ã�-![]() x2+3x+8=0��
x2+3x+8=0��
��ã�x18��x2=2��
�ߵ�E��x��ĸ������ϣ�
���E��-2��0����
��OE=2��
��������ã���D���˶�t��ʱ��BD=t��OC=t��
��OD=8��t��
��DE=OE+OD=10��t��
��S=![]() DEOC=
DEOC=![]() ��10-t��t=-
��10-t��t=-![]() t2+5t��
t2+5t��
��S=-![]() t2+5t=-
t2+5t=-![]() ��t-5��2+
��t-5��2+![]() ��
��
�൱t=5ʱ��S���=![]()
��3��
�ɣ�2��֪����t=5ʱ��S���=![]() ��
��
�൱t=5ʱ��OC=5��OD=3��
��C��0��5����D��3��0����
�ɹ��ɶ����ã�CD=![]() ��
��
��ֱ��CD�Ľ���ʽΪ��y=kx+b��
��C��0��5����D��3��0����������ʽ�ã�
k=-![]() ��b=5��
��b=5��
��ֱ��CD�Ľ���ʽΪ��y=-![]() x+5��
x+5��
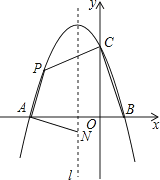
��E����EF��CD�������������P����ͼ1��

��ֱ��EF�Ľ���ʽΪ��y=-![]() x+b��
x+b��
��E��-2��0������ã�b=-![]() ��
��
��ֱ��EF�Ľ���ʽΪ��y=-![]() x-
x-![]() ��
��
��y=-![]() x-
x-![]() ����y=-
����y=-![]() x2+3x+8�����ɷ�����ã�
x2+3x+8�����ɷ�����ã�
 ��
��
��ã�![]() ��
�� ��
��
��P��![]() ����
����![]() ����
����
����E��EG��CD������ΪG��
�ߵ�t=5ʱ��S��ECD=![]() =
=![]() ��
��
��EG=![]() ��
��
����D��DN��CD������ΪN����ʹDN=![]() ������N��NM��x�ᣬ����ΪM����ͼ2��
������N��NM��x�ᣬ����ΪM����ͼ2��

�ɵá�EGD�ס�DMN��
��![]() ��
��
����![]() ��
��
��ã�DM=![]() ��
��
��OM=![]() ��
��
�ɹ��ɶ����ã�MN=![]() =
=![]() ��
��
��N��![]() ��
��![]() ����
����
����N��NH��CD���������߽����P����ͼ2��
��ֱ��NH�Ľ���ʽΪ��y=-![]() x+b��
x+b��
��N��![]() ��
��![]() ����������ʽ�ã�b=
����������ʽ�ã�b=![]() ��
��
��ֱ��NH�Ľ���ʽΪ��y=-![]() x+
x+![]() ��
��
��y=-![]() x+
x+![]() ����y=-
����y=-![]() x2+3x+8�����ɷ�����ã�
x2+3x+8�����ɷ�����ã�
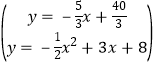 ��
��
��ã�![]() ��
�� ��
��
��P��8��0����P��![]() ��
��![]() ����
����
��������������CED��������ʱ�����������ϴ��ڵ�P����E���⣩��ʹ��PCD��������ڡ�CED������������P������Ϊ��P��![]() ��-
��-![]() ����P��8��0����P��
����P��8��0����P��![]() ��
��![]() ����
����
����������1������A��0��8����B��8��0������������y=��![]() x2+bx+c������������ߵĽ���ʽΪ��y=��
x2+bx+c������������ߵĽ���ʽΪ��y=��![]() x2+3x+8��
x2+3x+8��
��2����������ã���D���˶�t��ʱ��BD=t��OC=t��Ȼ���ɵ�A��0��8����B��8��0�����ɵ�OA=8��OB=8���Ӷ��ɵ�OD=8��t��Ȼ����y=0�������E������Ϊ����2��0���������ɵ�OE=2��DE=2+8��t=10��t��Ȼ�����������ε������ʽ�������CED�����S��D���˶�ʱ��t�ĺ�������ʽΪ��S=��![]() t2+5t��Ȼ��ת��Ϊ����ʽ���������ֵΪ��S���=
t2+5t��Ȼ��ת��Ϊ����ʽ���������ֵΪ��S���=![]() ��
��
��3���ɣ�2��֪����t=5ʱ��S���=![]() ��������֪����t=5ʱ��OC=5��OD=3�������ɵ�CD=
��������֪����t=5ʱ��OC=5��OD=3�������ɵ�CD=![]() ���Ӷ�ȷ��C��0��5����D��3��0��Ȼ����ݴ���ϵ�������ֱ��CD�Ľ���ʽΪ��y=��
���Ӷ�ȷ��C��0��5����D��3��0��Ȼ����ݴ���ϵ�������ֱ��CD�Ľ���ʽΪ��y=��![]() x+5��Ȼ���E����EF��CD�������������P��Ȼ�����ֱ��EF�Ľ���ʽ���������������������ü��ɵõ����е�һ����P�����꣬Ȼ����������������E��CD�ľ���Ϊ��
x+5��Ȼ���E����EF��CD�������������P��Ȼ�����ֱ��EF�Ľ���ʽ���������������������ü��ɵõ����е�һ����P�����꣬Ȼ����������������E��CD�ľ���Ϊ��![]() ��Ȼ�����D��DN��CD������ΪN����ʹDN=
��Ȼ�����D��DN��CD������ΪN����ʹDN=![]() ��Ȼ�����N�����꣬Ȼ�����N��NH��CD���������߽����P��Ȼ�����ֱ��NH�Ľ���ʽ����������������������⼴�ɵõ����е���������P�����꣮
��Ȼ�����N�����꣬Ȼ�����N��NH��CD���������߽����P��Ȼ�����ֱ��NH�Ľ���ʽ����������������������⼴�ɵõ����е���������P�����꣮