题目内容
已知反比例函数y=
图象过第二象限内的点A(-2,m),AB⊥x轴于B,Rt△AOB面积为2,若直线AC经过点A,并且经过反比例函数y=
的图象上另一点C(n,-
).
(1)反比例函数的解析式为______,m=______,n=______;
(2)求直线AC的解析式;
(3)在y轴上是否存在一点P,使△PAO为等腰三角形?若存在,请求出P点坐标;若不存在,说明理由.

| k |
| x |
| k |
| x |
| 3 |
| 2 |
(1)反比例函数的解析式为______,m=______,n=______;
(2)求直线AC的解析式;
(3)在y轴上是否存在一点P,使△PAO为等腰三角形?若存在,请求出P点坐标;若不存在,说明理由.

(1)∵Rt△AOB面积为2,
∴|k|=4,
则反比例函数的解析式是:y=-
;
把A(-2,m)代入y=-
得,m=-
=2;
把C(n,-
)代入y=
得:-
=-
,解得:n=
;
(2)设直线AC的解析式为y=ax+b,由(1)知A(-2,2),C(
,-
)
∵直线AC经过点A、B
∴
解得
∴直线AC的解析式y=-
x+
.
(3)答:存在点P使△PAO为等腰三角形;
∵点A(-2,2),AB=|2|=2,
∴OB=|-2|=2,在Rt△AOB中,OA=
=
=2
.
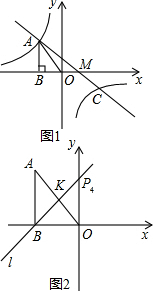
①以点O为圆心,以OA长为半径画弧,交y轴于点P1、P2,P1(0,-2
),P2(0,2
).(如图1)
②以点A为圆心,以OA长为半径画弧,交y轴于点P3、另一个交点与点O重合.由勾股定理算得P3(0,4).(如图1)
③作OA的垂直平分线l交y轴于P4,如图2,
∵AB=OB=2,∠ABO=90°,∴∠BOA=45°,∴∠P4OA=45°
∵直线l是OA的垂直平分线,∴∠P4KO=90°,OK=
OA.
∴∠KP4O=45°,OK=
×2
=
,∠P4OA=∠KP4O,OK=KP4=
.
∴由勾股定理求得OP4=2.点P4(0,2).
综上可知:满足条件的点P的坐标分别为:P1(0,-2
),P2(0,2
),P3(0,4),P4(0,2).
∴|k|=4,
则反比例函数的解析式是:y=-
| 4 |
| x |
把A(-2,m)代入y=-
| 4 |
| x |
| 4 |
| -2 |
把C(n,-
| 3 |
| 2 |
| 4 |
| x |
| 3 |
| 2 |
| 4 |
| n |
| 8 |
| 3 |
(2)设直线AC的解析式为y=ax+b,由(1)知A(-2,2),C(
| 8 |
| 3 |
| 3 |
| 2 |
∵直线AC经过点A、B
∴
|
解得
|
∴直线AC的解析式y=-
| 3 |
| 4 |
| 1 |
| 2 |
(3)答:存在点P使△PAO为等腰三角形;
∵点A(-2,2),AB=|2|=2,
∴OB=|-2|=2,在Rt△AOB中,OA=
| AB2+OB2 |
| 22+22 |
| 2 |
①以点O为圆心,以OA长为半径画弧,交y轴于点P1、P2,P1(0,-2
| 2 |
| 2 |
②以点A为圆心,以OA长为半径画弧,交y轴于点P3、另一个交点与点O重合.由勾股定理算得P3(0,4).(如图1)
③作OA的垂直平分线l交y轴于P4,如图2,
∵AB=OB=2,∠ABO=90°,∴∠BOA=45°,∴∠P4OA=45°
∵直线l是OA的垂直平分线,∴∠P4KO=90°,OK=
| 1 |
| 2 |
∴∠KP4O=45°,OK=
| 1 |
| 2 |
| 2 |
| 2 |
| 2 |
∴由勾股定理求得OP4=2.点P4(0,2).
综上可知:满足条件的点P的坐标分别为:P1(0,-2
| 2 |
| 2 |


练习册系列答案
相关题目




 b(k>0)与x轴交于点A(a,0)、与y轴交于点B.
b(k>0)与x轴交于点A(a,0)、与y轴交于点B.