Question

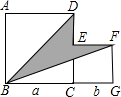
如图，有A、B、C三种不同型号的卡片，每种卡片各有k张．其中A型卡片是边长为a的正方形，B型卡片是长为b、宽为a的长方形，C型卡片是边长为b的正方形．从其中取若干张卡片，每种卡片至少取一张，把取出的这些卡片拼成一个正方形（所拼的图中既不能有缝隙，也不能有重合部分）．
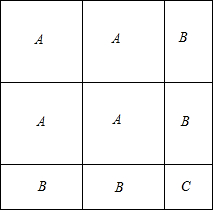
尝试操作：若k=10，请选取适当的卡片拼成一个边长为（2a+b）的正方形，画出示意图．
思考解释：若k=20，
①共取出50张卡片，取出的这些卡片能否拼成一个正方形？请简要说明理由；
②可以拼成______种不同的正方形．
拓展应用：上述A、B、C型的卡片各若干张（足够多），已知：a=2b，现共取出2500张卡片，拼成一个正方形，求可以拼成的正方形中面积最大值．（用含a的代数式表示）．

Answer 1

尝试操作：如图

思考解释：
①假设存在这样的正方形，不妨设这个正方形的边长为（xa+yb），则这个正方形的面积为（xa+yb）²=x²a²+2xyab+y²b²，
即此时需要x²张A卡片，2xy张B卡片，y²张C卡片，因此总共需要（x²+2xy+y²）张卡片，即（x+y）²张卡片．那么根据题意，（x+y）²=50，因此不存在这样的x、y满足题意，因此不能从其中取出50张卡片拼成正方形．
②13；
对本题给出方法如下：
法一：枚举法如（a+2b）²、（a+3b）²；
法二：由①知，令m=（x+y）²=x²+2xy+y²，则m为一个完全平方数，且满足

4≤m≤60 x2≤20 2xy≤20 y2≤20

，
1°m=4时，x+y=2，

x=1 y=1

1种；
2°m=9时，x+y=3，

x=1 y=2

x=2 y=1

2种；
3°m=16时，x+y=4，

x=1 y=3

x=2 y=2

x=3 y=1

3种；
4°m=25时，x+y=5，

x=1 y=4

x=2 y=3

x=3 y=2

x=4 y=1

4种；

5°m=36时，x+y=6，

x=2 y=4

x=3 y=3

x=4 y=2

3种；
6°m=49时，x+y=7，
0种
共13种．
拓展应用：
（x+y）²=2500，x+y=50，y=50-x，
边长为：xa+yb=xa+

a

2

（50-x）=（25+

x

2

）a，
25+

x

2

随x增大而增大，所以当x=49时最大．
最大面积为：（49a+b）²=（99b）²=（

99a

2

）²．