题目内容
【题目】已知直线![]() ,直线
,直线![]() 与直线
与直线![]() 、
、![]() 分别相交于点
分别相交于点![]() 、
、![]() .
.
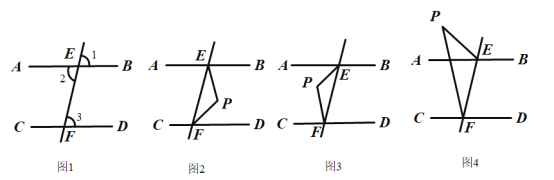
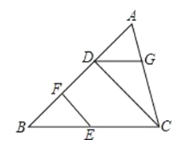
(1)如图1,若![]() ,求
,求![]() ,
,![]() 的度数;
的度数;
(2)若点![]() 是平面内的一个动点,连接
是平面内的一个动点,连接![]() 、
、![]() ,探索
,探索![]() 、
、![]() 、
、![]() 之间的数量关系;
之间的数量关系;
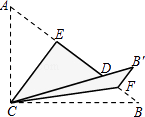
①当点![]() 在图2的位置时,请写出
在图2的位置时,请写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明;
之间的数量关系并证明;
②当点![]() 在图3的位置时,请写出
在图3的位置时,请写出![]() 、
、![]() 、
、![]() 之间的数量关系并证明;
之间的数量关系并证明;
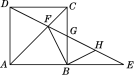
③当点![]() 在图4的位置时,请直接写出
在图4的位置时,请直接写出![]() 、
、![]() 、
、![]() 之间的数量关系.
之间的数量关系.
【答案】(1)![]() ;(2)①
;(2)①![]() ,证明见解析;②
,证明见解析;②![]() ,证明见解析;③
,证明见解析;③![]() 或
或![]() .
.
【解析】
(1)根据对顶角相等求∠2,根据两直线平行,同位角相等求∠3;
(2)①过点P作MN∥AB,根据平行线的性质得∠EPM=∠PEB,且有MN∥CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB+∠PFD.
②③的解题方法与①一样,分别过点P作MN∥AB,然后利用平行线的性质得到三个角之间的关系.
(1)解:∵![]() ,
,![]() ,
,
∴![]() ;
;
∵![]() ,
,
∴![]() .
.
(2)①![]() .
.
过点![]() 作
作![]() ,则
,则![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
即![]() .
.
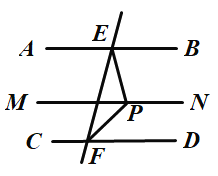
②![]() ,
,
过点![]() 作
作![]() ,则
,则![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.
即![]() .
.
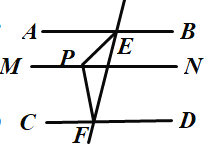
③![]() 或
或![]() .写对一种即可.
.写对一种即可.
理由:如图4,过点P作PM∥AB,
∵AB∥CD,MP∥AB,
∴MP∥CD,
∴∠PEB=∠MPE,∠PFD=∠MPF,
∵∠EPF+∠FPM=∠MPE,
∴∠EPF+∠PFD=∠PEB.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】小明利用课余时间回收废品,将卖得的钱去购买5本大小不同的两种笔记本,要求共花钱不超过28元,且购买的笔记本的总页数不低于340页,两种笔记本的价格和页数如下表.为了节约资金,小明应选择哪一种购买方案?请说明理由.
大笔记本 | 小笔记本 | |
价格(元/本) | 6 | 5 |
页数(页/本) | 100 | 60 |