题目内容
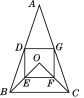
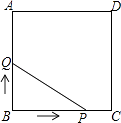
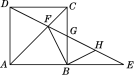
【题目】如图,E为正方形ABCD的边AB的延长线上一点,DE交AC于点F,交BC于点G,H为GE的中点.
求证:FB⊥BH.
【答案】证明见解析
【解析】
根据正方形的性质,用SAS判定△DCF≌△BCF,从而得到对应角相等,再根据中线的性质及角之间的关系便可推出FB⊥BH..
证明:∵四边形ABCD是正方形,
∴CD=CB,∠DCF=∠BCF=45°,
DC∥AE,∠CBE=90°,
∴∠CDF=∠E.
又∵CF=CF,∴△DCF≌△BCF.
∴∠CDF=∠CBF.∴∠CBF=∠E.
∵H为GE的中点,
∴HB=HG=![]() GE.
GE.
∴∠HGB=∠HBG.
∵∠CDG+∠CGD=90°,∠CGD=∠HGB=∠HBG,
∴∠FBG+∠HBG=90°,
即∠FBH=90°,∴FB⊥BH.

练习册系列答案
相关题目
【题目】亚健康是时下社会热门话题,进行体育锻炼是远离亚健康的一种重要方式,为了解某市初中学生每天进行体育锻炼的时间情况,随机抽样调查了100名涌中学生,根据调查结果得到如图所示的统计图表.
类别 | 时间t(小时) | 人数 |
A | t≤0.5 | 5 |
B | 0.5<t≤1 | 20 |
C | 1<t≤1.5 | a |
D | 1.5<t≤2 | 30 |
E | t>2 | 10 |
请根据图表信息解答下列问题: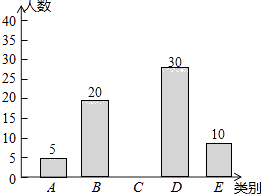
(1)a=;
(2)补全条形统计图;
(3)据了解该市大约有30万名初中学生,请估计该市初中学生每天进行体育锻炼时间在1小时以上的人数.