��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���ֱ��x=![]() �Գ����������y=ax2+bx+c��ֱ��l��y=kx+m��k��0������A��1��1����B���㣬��y�ύ��C��0��5����ֱ��l��y�ύ�ڵ�D��
�Գ����������y=ax2+bx+c��ֱ��l��y=kx+m��k��0������A��1��1����B���㣬��y�ύ��C��0��5����ֱ��l��y�ύ�ڵ�D��
��1���������ߵĺ�������ʽ��
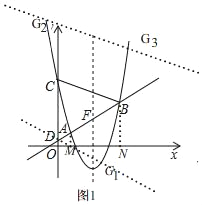
��2����ֱ��l�������ߵĶԳ���Ľ���ΪF��G����������λ�ڶԳ����Ҳ��һ�㣬��![]() ������BCG����BCD�����ȣ����G�����ꣻ
������BCG����BCD�����ȣ����G�����ꣻ
��3������x�������ҽ���һ��P��ʹ��APB=90������k��ֵ��

���𰸡���1��y=x2��5x+5����2��G��3����1����G��![]() ��
��![]() ������3����1+
������3����1+![]()
��
��������
��1�����ݶ��κ�����ͼ����ϵ���Ĺ�ϵ�г���������a��b��c��ֵ���ö��κ����Ľ���ʽ��
��2����AM��x�ᣬBN��x�ᣬ����ֱ�ΪM��N���ɵó�B������꼴���г����������һ�κ�������ʽ���ٸ���S��BCD=S��BCG�г���ʽ�������G��
��3�����������г���ʽ���x��ֵ����B��k+4��k2+3k+1�����ٸ�����ABΪֱ����Բ��x��ֻ��һ�����㣬��PΪ�е㣬�ó�O��P��x�ᣬP��![]() ��0����������AMP�ס�PNB���ó�AMBN=PNPM��������ֵ�������k��ֵ.
��0����������AMP�ס�PNB���ó�AMBN=PNPM��������ֵ�������k��ֵ.
�⣺��1��������ɵ�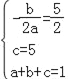 ��
��
���a=1��b=��5��c=5��
����κ����Ľ���ʽΪ��y=x2��5x+5��
��2����AM��x�ᣬBN��x�ᣬ����ֱ�ΪM��N��
��![]() ��
��
��MQ=![]() ��
��
��NQ=2��B��![]() ��
��![]() ����
����
��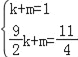 ��
��
���![]() ��
��
��![]() ��D��0��
��D��0��![]() ����
����
ͬ������![]() ��
��
��S��BCD=S��BCG��
���DG��BC��G��BC�·�����![]() ��
��
��![]() =x2��5x+5��
=x2��5x+5��
��ã�![]() ��x2=3��
��x2=3��
��x��![]() ��
��
��x=3��
��G��3����1����
��G��BC�Ϸ�ʱ��ֱ��G2G3��DG1����BC�Գƣ�
��![]() =
=![]() ��
��
![]() =x2��5x+5��
=x2��5x+5��
���![]() ��
��![]() ��
��
��x��![]() ��
��
��x=![]() ��
��
��G��![]() ��
��![]() ����
����
����������G������ΪG��3����1����G��![]() ��
��![]() ����
����
��3���������֪��k+m=1��
��m=1��k��
��yl=kx+1��k��
��kx+1��k=x2��5x+5��
��ã�x1=1��x2=k+4��
��B��k+4��k2+3k+1����
��AB�е�ΪO�䣬
��P������ֻ��һ����
����ABΪֱ����Բ��x��ֻ��һ�����㣬��PΪ�е㣬
��O��P��x�ᣬ
��PΪMN���е㣬
��P��![]() ��0����
��0����
�ߡ�AMP�ס�PNB��
��![]() ��
��
��AMBN=PNPM��
��1����k2+3k+1��=��k+4��![]() ����
����![]() ����
����
��k��0��
��k=![]() =��1+
=��1+![]() ��
��

 ÿ��10���ӿ�����������������ϵ�д�
ÿ��10���ӿ�����������������ϵ�д�







