题目内容
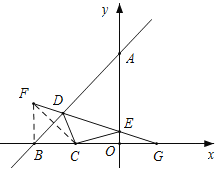
【题目】如图所示,直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,D、E分别是直线AB、y轴上的动点,当△CDE周长最小时,点D的坐标为_____.

【答案】(﹣![]() ,
,![]() ).
).
【解析】
作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,由轴对称的性质,可得DF=DC,EC=EG,故当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,此时△DEC周长最小;
解:如图,作点C关于AB的对称点F,关于AO的对称点G,连接DF,EG,
∵直线y=x+2与两坐标轴分别交于A、B两点,点C是OB的中点,
∴B(﹣2,0),C(﹣1,0),
∴BO=2,OG=1,BG=3,
易得∠ABC=45°,
∴△BCF是等腰直角三角形,
∴BF=BC=1,
由轴对称的性质,可得DF=DC,EC=EG,
当点F,D,E,G在同一直线上时,△CDE的周长=CD+DE+CE=DF+DE+EG=FG,
此时△DEC周长最小,
设直线FG的解析式为:y=kx+b,
∵F(﹣2,1),G(1,0),
∴![]() ,
,
∴![]() ,
,
直线FG的解析式为:![]() ,
,
解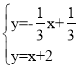 得
得![]() ,
,
∴点D的坐标为(﹣![]() ,
,![]() ),
),
故答案为:(﹣![]() ,
,![]() ).
).

练习册系列答案
相关题目