Question

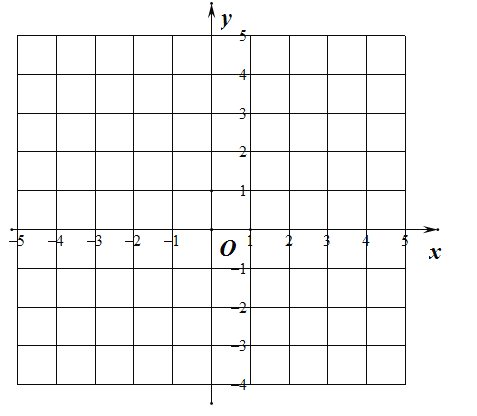
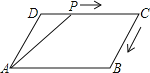
【题目】如图，矩形的顶点、分别在轴，轴上，顶点在第二象限，点的坐标为．将线段绕点逆时针旋转至线段，若反比例函数y=（k≠0）的图象经过A、D两点，则k值为_________．

Answer 1

【答案】-．

【解析】

过点D作DE⊥x轴于点E，由点B的坐标为（-2，0）知OC=AB=-，由旋转性质知OD=OC=-、∠DOC=60°，据此求得OE=ODcos30°=-k，DE=ODsin30°=-k，即D（k，-k），代入解析式解之可得．

解：过点D作DE⊥x轴于点E，

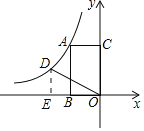
∵点B的坐标为（-2，0），
∴AB=-，
∴OC=-，
由旋转性质知OD=OC=-、∠COD=60°，
∴∠DOE=30°，
∴DE=OD=-k，OE=ODcos30°= k，
即D（k，-k），
∵反比例函数y=（k≠0）的图象经过D点，
∴k=（k）（-k）=- k2，
解得：k=0（舍）或k=- ，
故答案为：-．