题目内容
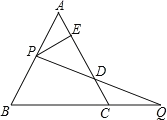
【题目】如图,已知过点B(1,0)的直线l1与直线l2:y=2x+4相交于点P(﹣1,a),l1与y轴交于点C,l2与x轴交于点A.

(1)求a的值及直线l1的解析式.
(2)求四边形PAOC的面积.
(3)在x轴上方有一动直线平行于x轴,分别与l1,l2交于点M,N,且点M在点N的右侧,x轴上是否存在点Q,使△MNQ为等腰直角三角形?若存在,请直接写出满足条件的点Q的坐标;若不存在,请说明理由.
【答案】(1)a=2,y=﹣x+1;(2)四边形PAOC的面积为![]() ;(3)点Q的坐标为
;(3)点Q的坐标为![]() 或
或![]() 或(﹣
或(﹣![]() ,0).
,0).
【解析】
(1)将点P的坐标代入直线l2解析式,即可得出a的值,然后将点B和点P的坐标代入直线l1的解析式即可得解;
(2)作PE⊥OA于点E,作PF⊥y轴,然后由△PAB和△OBC的面积即可得出四边形PAOC的面积;
(3)分类讨论:①当MN=NQ时,②当MN=MQ时,③当MQ=NQ时,分别根据等腰直角三角形的性质,结合坐标即可得解.
(1)∵y=2x+4过点P(﹣1,a),
∴a=2,
∵直线l1过点B(1,0)和点P(﹣1,2),
设线段BP所表示的函数表达式y=kx+b并解得:
函数的表达式y=﹣x+1;
(2)过点P作PE⊥OA于点E,作PF⊥y轴交y轴于点F,
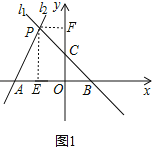
由(1)知,AB=3,PE=2,OB=1,点C在直线l1上,
∴点C坐标为(0,1),
∴OC=1
则![]() ;
;
(3)存在,理由如下:
假设存在,如图,设M(1﹣a,a),点N![]() ,
,
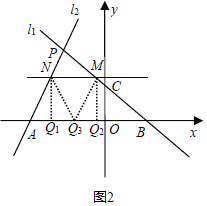
①当MN=NQ时,
![]()
∴![]()
∴![]() ,
,
②当MN=MQ时,
∴![]()
∴![]() ,
,
③当MQ=NQ时,![]() ,
,
∴![]() ,
,
∴![]() .
.
综上,点Q的坐标为:![]() 或
或![]() 或(﹣
或(﹣![]() ,0).
,0).

练习册系列答案
相关题目