��Ŀ����
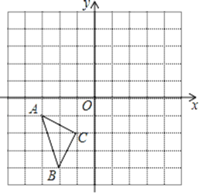
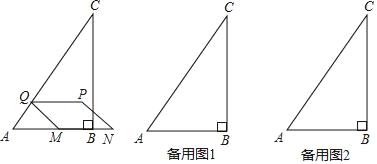
����Ŀ����ͼ����֪��Rt��ABC�У���ABC=90�㣬AB=6��BC=8������M��ÿ��2����λ���ٶȴӵ�A����������A��B��C�ķ����˶�������M�����Cʱ���˶�ֹͣ����N�ǵ�M���ڵ�B�ĶԳƵ㣬����M��MQ��AC�ڵ�Q����MN��MQΪ����MNPQ�����M���˶�ʱ��Ϊt�룮
��1���ֱ���t=2��t=5ʱ���߶�MN�ij���
��2���Ƿ����������t��ֵ��ʹ��MNPQΪ���Σ������ڣ������t��ֵ���������ڣ���˵�����ɣ�
��3������P����ֱ��MQ�ĶԳƵ�P'������P'������ABC�ڲ�ʱ����ֱ��д��t��ȡֵ��Χ��
���𰸡���1��8��2����t=![]() ��
��![]() ʱ���ı���MNPQΪ���Σ�3��2��t��3��3��t��
ʱ���ı���MNPQΪ���Σ�3��2��t��3��3��t��![]() ʱ������P'������ABC�ڲ�
ʱ������P'������ABC�ڲ�
��������
��1��t=2ʱ����M���߶�AB�ϣ����AM���ɣ�t=5ʱ����M���߶�BC�ϣ����BM���ɽ�����⣻
��2�����������Σ��ֱ��������������ε����ʹ������̼��ɽ�����⣻
��3�����������Σ�����ͼ3�У�����P����QM�ĶԳƵ�P�������߶�AB��ʱ������ͼ4�У�����P�ĶԳƵ������߶�BC��ʱ���ֱ����t��ֵ���ɽ������.
��1���������t=2��AM=4��MB=2��
��M��N���ڵ�B�Գƣ�
��BM=BN��
��MN=2BM=4
t=5��AB+BM=10��AB=6��MB=4��
��MN=2BM=8��
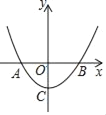
��2�����һ������M�ڱ�AB��ʱ����ͼ1��
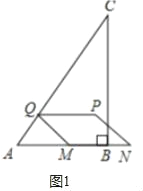
����AQM�ס�ABC���ɵ�![]() =
=![]() ��
��
��AM=2t��AB=6��BC=8��AC=10��
��QM=![]() t��BM=6��2t��MN=12��4t��
t��BM=6��2t��MN=12��4t��
QM=MNʱ����![]() t=12��4t��
t=12��4t��
���t=![]() ��
��
�����������M�ڱ�BC��ʱ����ͼ2��
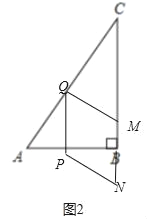
��CMQ�ס�CAB��
��![]() ��
��
��![]() ��
��
��MQ=![]() ��14��2t����
��14��2t����
��MN=MQ��
��2��2t��6��=![]() ��14��2t����
��14��2t����
��ã�t=![]()
���ϣ���t=![]() ��
��![]() ʱ���ı���MNPQΪ���Σ�
ʱ���ı���MNPQΪ���Σ�
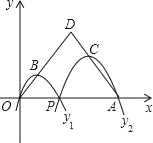
��3����ͼ3�У�
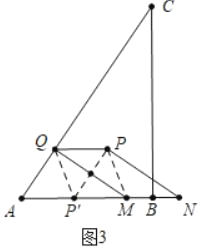
����P����QM�ĶԳƵ�P�������߶�AB��ʱ����֤�ı���PQP��M�����Σ�
��PP����MQ����MQ��AC��
��PP����AC����PQ��AP��
���ı���AQPP����ƽ���ı��Σ�
��AP��=PQ=MP��=MN��
��AM=2MN��
��2t=2��6��2t��
��t=2��
��
��ͼ4��
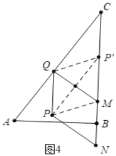
����P�ĶԳƵ������߶�BC��ʱ����֤�ı���PQP��M�����Σ�
�ɵ�P��M=P��Q=CP��=MN��
��BM+CM=8��
��2t��6+2��4t��12��=8��
���t=![]() ��
��
��3��t��![]() ʱ������P'������ABC�ڲ���
ʱ������P'������ABC�ڲ���
����������2��t��3��3��t��![]() ʱ������P'������ABC�ڲ���
ʱ������P'������ABC�ڲ���

 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д� ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�