题目内容
【题目】如图1，甲、乙两个容器内都装了一定数量的水，现将甲容器中的水匀速倒入乙容器中. 图2中，线段AB、线段CD分别表示容器中的水的深度h（厘米）与倒入时间t（分钟）的函数图像.
（1）请说出点C的纵坐标的实际意义；
（2）经过多长时间，甲、乙两个容器中的水的深度相等？
（3）如果甲容器的底面积为10cm2，求乙容器的底面积.
【答案】（1）点C的纵坐标的实际意义是乙容器中原有的水的深度是5cm；（2）2分钟后，两容器内水得深度相等.（3）20cm2.
【解析】试题分析：
（1）由题意可知，点C的纵坐标表示乙容器中原有水的深度；
（2）先分别求出直线AB和直线CD的解析式，解由两个解析式组成的方程组，即可得到两容器中水的深度相等的时间；
（3）先由图中信息计算出甲容器内原有水的体积，而根据图中信息可知，将甲容器内的水全部倒入乙容器后，其深度增加了10cm，由此即可计算出乙容器的底面积.
试题解析：
（1）点C的纵坐标的实际意义是乙容器中原有的水的深度是5cm；
（2）设直线AB的解析式为： 
，由图中信息可得： 
，解得
，
∴直线AB的函数关系式为： 
；
同理可求得直线CD的函数关系式为： 
；
由： 
，解得： 
，
∴2分钟后，两容器内水得深度相等；
（3）∵容器甲的底面积为10cm2，容积甲中原有水的深度为20cm，
∴容器甲中原有的水的体积为10×20=200cm3，
又∵在将甲容器中的水倒入乙容器中后，容器乙中水的深度的增加值为15-5=10cm，
∴容器乙的底面积为200÷10=20 cm2.
小学课堂作业系列答案
金博士一点全通系列答案【题目】按下列程序计算，把答案填写在表格里，然后看看有什么规律，想想为什么会有
这个规律？
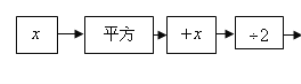
（1）填写表内空格：
输入 | 3 | 2 | －2 |
| … |
输出答案 | 0 | … |
（2）你发现的规律是____________.
（3）用简要过程说明你发现的规律的正确性.
