Question

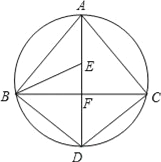
【题目】如图,⊙O 的半径为１,直线CD 经过圆心O,交⊙O 于C、D 两点,直径AB⊥CD,点 M 是直线CD 上异于点C、O、D 的一个动点,AM 所在的直线交⊙O 于点N,点 P 是直线CD 上另一点,且PM＝PN．

(1)当点 M 在⊙O 内部,如图①,试判断 PN 与⊙O 的关系,并写出证明过程;

(2)当点 M 在⊙O 外部,如图②,其他条件不变时,(1)的结论是否还成立? 请说明理由;

(3)当点 M 在⊙O 外部,如图③,∠AMO＝15°,求图中阴影部分的面积．

Answer 1

【答案】(1)详见解析；（2）成立，理由详见解析；（3）＋－．

【解析】试题分析：（1）PN 与⊙O 相切．要证明ONPN即可，连接ON，PM＝PN，所以∠PNM＝∠PMN，∠AMO＝∠PMN，AB⊥CD,所以∠PMN+∠MAO=90°，又因∠MAO=∠MNO,所以∠PNM+∠MNO=90°，所以PN 与⊙O 相切．（2）成立，进行等量代换，∠MAO+∠OMA=90°，因∠OMA=∠PNM，∠MAO=∠ONA,所以∠PNM+∠ONA=90°，所以∠ONP=90°；（3）阴影部分的面积可通过SAOC+S扇形AOC-SAON求得.

(1)PN 与⊙O 相切．证明：连接ON，则∠ONA＝∠OAN．

∵PM＝PN，∴∠PNM＝∠PMN．又∵∠AMO＝∠PMN，

∴∠PNM＝∠AMO．

∴∠PNO＝∠PNM＋∠ONA＝∠AMO＋∠OAN＝90°，即PN 与⊙O 相切．

(2)成立．理由如下：连接ON，则∠ONA＝∠OAN．

∵PM＝PN，∴∠PNM＝∠PMN．

在Rt△AOM中,∠OMA＋∠OAM＝90°．∴∠PNM＋∠ONA＝90°,

∴∠PNO＝180°－90°＝90°．即PN 与⊙O 相切．

(3)连接ON，由(2)可知∠ONP＝90°．

∵∠AMO＝15°，PM＝PN，∴∠PNM＝15°，∠OPN＝30°，

∴∠PON＝60°,∠AON＝30°．

过点N 作NE⊥OD，垂足为点E．则OE＝．∴NE＝．

∴S阴影＝S△AOC＋S扇形AON－S△CON＝OC·OA＋－CO·NE

＝＋－

∴图中阴影部分的面积为＋－