题目内容
【题目】△ABC是等腰三角形，腰上的高为8cm，面积为40cm2，则该三角形的周长是_______cm.
【答案】
或
.
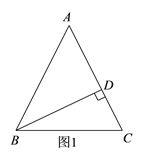
【解析】（1）如图1，在△ABC中，AB=AC，∠A是锐角，BD是AC边上的高，
由题意可知：BD=8cm，S△ABC=
BD·AC=40cm2，
∴AC=10cm=BC，
∴在Rt△ABD中，由勾股定理可得：AD=
（cm），
∴DC=AC-AD=4cm，
∴在Rt△BDC中，由勾股定理可得：BC=
（cm），
∴此时△ABC的周长=AB+AC+BC=
（cm）；
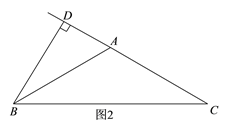
（2）如图2，当顶角∠BAC为钝角时，同理可解得△ABC的周长=AB+AC+BC=
（cm）；
综合（1）、（2）可得△ABC的周长为： 
（cm）或
（cm）.
故答案为： 
或
.
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
