题目内容
【题目】荣庆公司计划从商店购买同一品牌的台灯和手电筒，已知购买一个台灯比购买一个手电筒多用20元，若用400元购买台灯和用160元购买手电筒，则购买台灯的个数是购买手电筒个数的一半．
（1）求购买该品牌一个台灯、一个手电筒各需要多少元？
（2）经商谈，商店给予荣庆公司购买一个该品牌台灯赠送一个该品牌手电筒的优惠，如果荣庆公司需要手电筒的个数是台灯个数的2倍还多8个，且该公司购买台灯和手电筒的总费用不超过670元，那么荣庆公司最多可购买多少个该品牌台灯？
【答案】（1）购买一个台灯需要25元，购买一个手电筒需要5元；（2）荣庆公司最多可购买21个该品牌的台灯．
【解析】
试题分析：（1）设购买该品牌一个手电筒需要x元，则购买一个台灯需要（x+20）元．则根据等量关系：购买台灯的个数是购买手电筒个数的一半，列出方程；
（2）设公司购买台灯的个数为a，则还需要购买手电筒的个数是（2a+8）个，则根据“该公司购买台灯和手电筒的总费用不超过670元”列出不等式．
解：（1）设购买该品牌一个手电筒需要x元，则购买一个台灯需要（x+20）元．
根据题意 得 
=
×
解得 x=5
经检验，x=5是原方程的解．
所以 x+20=25．
答：购买一个台灯需要25元，购买一个手电筒需要5元；
（2）设公司购买台灯的个数为a，则还需要购买手电筒的个数是（2a+8﹣a）
由题意得 25a+5（2a+8﹣a）≤670
解得 a≤21
∴荣庆公司最多可购买21个该品牌的台灯．
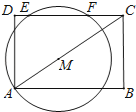
寒假创新型自主学习第三学期寒假衔接系列答案【题目】如图、矩形ABCD中，AB=8，AD=6．点M是对角线AC上的一个动点，以M点为圆心，线段AM长为半径画一个⊙M，若⊙M在以C为端点的矩形ABCD边上截得的线段EF=
AM，则线段AM的长是 ．
【题目】二次函数y=ax2+bx+c（a、b、c为常数，且a≠0）中的x与y的部分对应值如下表：
x | … | 0 | 1 | 2 | … |
y | … | 4 | ﹣4 | 6 | … |
（1）ac＜0；（2）当x＞1时，y的值随x值得增大而增大；（3）﹣1是方程ax2+bx+c=0的一个根；（4）当﹣1＜x＜2时，ax2+bx+c＜0，其中正确的个数为（ ）
A．4个 B．3个 C．2个 D．1个
