题目内容
【题目】如图.在平面直角坐标系中,点A(3,0),B(0,﹣4),C是x轴上一动点,过C作CD∥AB交y轴于点D.
(1)![]() 的值是 .
的值是 .
(2)若以A,B,C,D为顶点的四边形的面积等于54,求点C的坐标.
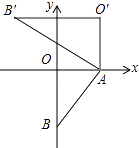
(3)将△AOB绕点A按顺时针方向旋转90°得到△AO′B′,设D的坐标为(0,n),当点D落在△AO′B′内部(包括边界)时,求n的取值范围.(直接写出答案即可)
【答案】
(1)![]()
(2)
解:设OC=3x,则OD=4x,
则AC=3+3x,BD=4+4x,
当A在x轴负半轴上时:
∵四边形ABCD的面积是54,
∴ ![]() ACBD=54,即
ACBD=54,即 ![]() (3+3x)(4+4x)=54,
(3+3x)(4+4x)=54,
解得:x=2或﹣4(舍去).
则C的坐标是(﹣6,0);
当A在x轴的正半轴上时,S四边形ABCD= ![]() ×3a4a﹣
×3a4a﹣ ![]() ×3×4=54,
×3×4=54,
解得:a= ![]() 或﹣
或﹣ ![]() (舍去).
(舍去).
则C的坐标是(3 ![]() ,0)
,0)
(3)
解:O′的坐标是(3,3),
则O′B′与y轴的交点坐标是(0,3);
则B′的坐标是(﹣1,3).
设AB′的解析式是y=kx+b,
根据题意得: ![]() ,
,
解得: 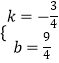 ,
,
则函数的解析式是y=﹣ ![]() x+
x+ ![]() ,
,
当x=0时,y= ![]() .即直线AB′与y轴的交点是(0,
.即直线AB′与y轴的交点是(0, ![]() ).
).
则n的范围是 ![]() ≤n≤3.
≤n≤3.
【解析】解:(1)∵A的坐标是(3,0),B的坐标是(0,﹣4),
∴OA=3,OB=4.
∵CD∥AB,
∴△AOB∽△COD,
∴ ![]() =
= ![]() =
= ![]() ;
;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目