题目内容
【题目】如图,正方形ABCD的顶点A,B与正方形EFGH的顶点G,H同在一段抛物线上,且抛物线的顶点同时落在CD和y轴上,正方形边AB与EF同时落在x轴上,若正方形ABCD的边长为4,则正方形EFGH的边长为 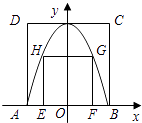
【答案】2 ![]() ﹣2
﹣2
【解析】解:∵正方形ABCD边长为4,
∴顶点坐标为:(0,4),B(2,0),
设抛物线解析式为:y=ax2+4,
将B点代入得,0=4a+4,
解得a=﹣1,
∴抛物线解析式为:y=﹣x2+4
设G点坐标为:(m,﹣m2+4),
则2m=﹣m2+4,
整理的:m2+2m﹣4=0,
解得:m1=﹣1+ ![]() ,a2=﹣1﹣
,a2=﹣1﹣ ![]() (不合题意舍去),
(不合题意舍去),
∴正方形EFGH的边长FG=2m=2 ![]() ﹣2.
﹣2.
所以答案是:2 ![]() ﹣2.
﹣2.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.

【题目】我市某中学为备战省运会,在校运动队的学生中进行了全能选手的选拔,并将参加选拔学生的综合成绩分成四组,绘成了如下尚不完整的统计图表.
组别 | 成绩 | 组中值 | 频数 |
第一组 | 90≤x<100 | 95 | 4 |
第二组 | 80≤x<90 | 85 | m |
第三组 | 70≤x<80 | 75 | n |
第四组 | 60≤x<70 | 65 | 21 |
根据图表信息,回答下列问题:
(1)参加活动选拔的学生共有人;表中m= , n=;
(2)若将各组的组中值视为该组的平均值,请你估算参加选拔学生的平均成绩;
(3)将第一组中的4名学生记为A、B、C、D,由于这4名学生的体育综合水平相差不大,现决定随机挑选其中两名学生代表学校参赛,试通过画树形图或列表的方法求恰好选中A和B的概率. 
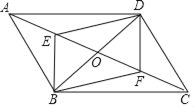
【题目】如图,ABCD的对角线AC、BD交于点O,E、F分别是AO、CO的中点,连接BE、DE、DF、BF,
(1)求证:四边形EBFD是平行四边形.
(2)求证:当AC=2BD时,四边形EBFD是矩形.
【题目】一只不透明的袋子中装有4个质地、大小均相同的小球,这些小球分别标有数字3,4,5,x.甲、乙两人每次同时从袋中各随机摸出1个球,并计算摸出的这2个小球上数字之和,记录后都将小球放回袋中搅匀,进行重复试验.实验数据如下表:
摸球总次数 | 10 | 20 | 30 | 60 | 90 | 120 | 180 | 240 | 330 | 450 |
“和为8”出现的频数 | 2 | 10 | 13 | 24 | 30 | 37 | 58 | 82 | 110 | 150 |
“和为8”出现的频率 | 0.20 | 0.50 | 0.43 | 0.40 | 0.33 | 0.31 | 0.32 | 0.34 | 0.33 | 0.33 |
解答下列问题:
(1)如果实验继续进行下去,根据上表数据,出现“和为8”的频率将稳定在它的概率附近.估计出现“和为8”的概率是;
(2)当x=7时,请用列表法或树状图法计算“和为8”的概率;并判断x=7是否可能.




