题目内容
【题目】如图,△ABC中,D、E在AB上,且D、E分别是AC、BC的垂直平分线上一点;若△CDE的周长为4,则AB的长为___________;若∠ACB=100°,则∠DCE=_________度; 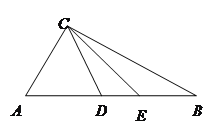
【答案】AB=4 ∠DCE=20°
【解析】
根据线段垂直平分线的性质,可得DC=DA,EC=EB,然后由△CDE的周长=DC+DE+EC=4,可得DA+DE+EB=4,即AB的长为4;然后根据三角形的内角和定理,由∠ACB=100°,求得∠A+∠B=80°,再由DC=DA,根据“等边对等角”可得∠DCA=∠A,同理∠ECB=∠B,即∠DCA+∠ECB=80°,最后可求得∠DCE=100°-80°=20°.
故答案为:4;20°.

练习册系列答案
相关题目
【题目】体育委员统计了全班同学60秒跳绳的次数,并列出下列人数次数分布表,回答下列问题:
次数x | 人数 |
60≤x<80 | 2 |
80≤x<100 | 5 |
100≤x<120 | 21 |
120≤x<140 | 13 |
140≤x<160 | 8 |
160≤x<180 | 4 |
(1)全班有多少人?
(2)组距、组数是多少?
(3)跳绳次数在100≤x<140范围内同学有多少人,占全班的百分之几(精确到0.01%)?