Question

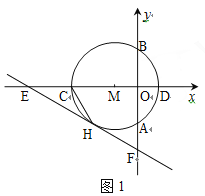
【题目】如图1，以点M（－1，0）为圆心的圆与y轴、x轴分别交于点A、B、C、D，直线y＝－x－与⊙M相切于点H，交x轴于点E，交y轴于点F．

（1）请直接写出OE、⊙M的半径r、CH的长；

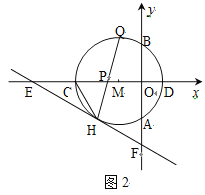
（2）如图2，弦HQ交x轴于点P，且DP : PH＝3 : 2，求cos∠QHC的值；

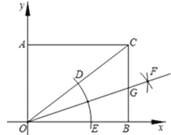
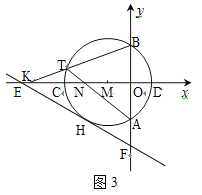
（3）如图3，点K为线段EC上一动点（不与E、C重合），连接BK交⊙M于点T，弦AT交x轴于点N．是否存在一个常数a，始终满足MN·MK＝a，如果存在，请求出a的值；如果不存在，请说明理由．

Answer 1

【答案】（1）OE=5，r=2，CH=2

（2）；

（3）a=4

【解析】

（1）在直线y＝－x－中，令y=0，可求得E的坐标，即可得到OE的长为5；连接MH，根据△EMH与△EFO相似即可求得半径为2；再由EC=MC=2，∠EHM=90°，可知CH是RT△EHM斜边上的中线，根据直角三角形斜边上的中线等于斜边的一半即可得出CH的长；

（2）连接DQ、CQ．根据相似三角形的判定得到△CHP∽△QPD，从而求得DQ的长，在直角三角形CDQ中，即可求得∠D的余弦值，即为cos∠QHC的值；

（3）连接AK，AM，延长AM，与圆交于点G，连接TG，由圆周角定理可知，

∠GTA=90°，∠3=∠4，故∠AKC=∠MAN，再由△AMK∽△NMA即可得出结论．

（1）OE=5，r=2，CH=2

（2）如图1，连接QC、QD，则∠CQD =90°，∠QHC =∠QDC，

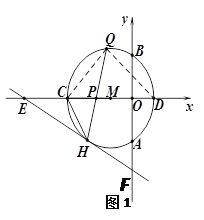
易知△CHP∽△DQP，故，得DQ=3，由于CD=4，

；

（3）如图2，连接AK，AM，延长AM，

与圆交于点G，连接TG，则

，

由于，故，；

而，故

在和中，；

故△AMK∽△NMA

;

即：

故存在常数，始终满足

常数a="4"

解法二：连结BM，证明∽

得