题目内容
【题目】如图①,AB是⊙O的直径,CD为弦,且AB⊥CD于E,点M为![]() 上一动点(不包括A,B两点),射线AM与射线EC交于点F.
上一动点(不包括A,B两点),射线AM与射线EC交于点F.
(1)如图②,当F在EC的延长线上时,求证:∠AMD=∠FMC.
(2)已知,BE=2,CD=8.
①求⊙O的半径;
②若△CMF为等腰三角形,求AM的长(结果保留根号).

【答案】(1)详见解析;(2)5;②8或![]()
【解析】
(1)想办法证明∠AMD=∠ADC,∠FMC=∠ADC即可解决问题;
(2)①在Rt△OCE中,利用勾股定理构建方程即可解决问题;
②分两种情形讨论求解即可.
解:(1)证明:如图②中,连接AC、AD.
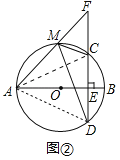
∵AB⊥CD,
∴CE=ED,
∴AC=AD,
∴∠ACD=∠ADC,
∵∠AMD=∠ACD,
∴∠AMD=∠ADC,
∵∠FMC+∠AMC=180°,∠AMC+∠ADC=180°,
∴∠FMC=∠ADC,
∴∠FMC=∠ADC,
∴∠FMC=∠AMD.
(2)解:①如图②﹣1中,连接OC.设⊙O的半径为r.
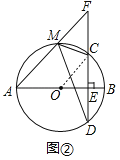
在Rt△OCE中,∵OC2=OE2+EC2,
∴r2=(r﹣2)2+42,
∴r=5.
②∵∠FMC=∠ACD>∠F,
∴只有两种情形:MF=FC,FM=MC.
如图③中,当FM=FC时,易证明CM∥AD,
∴![]() ,
,
∴AM=CD=8.

如图④中,当MC=MF时,连接MO,延长MO交AD于H.

∵∠MFC=∠MCF=∠MAD,∠FMC=∠AMD,
∴∠ADM=∠MAD,
∴MA=MD,
∴![]() ,
,
∴MH⊥AD,AH=DH,
在Rt△AED中,AD=![]() ,
,
∴AH=![]() ,
,
∵tan∠DAE=![]() ,
,
∴OH=![]() ,
,
∴MH=5+![]() ,
,
在Rt△AMH中,AM=![]() .
.

练习册系列答案
相关题目