Question

【题目】在△ABC中，∠C=90°，AC=BC，点D在射线BC上（不与点B、C重合），连接AD，将AD绕点D顺时针旋转90°得到DE，连接BE．

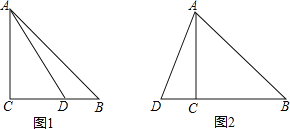
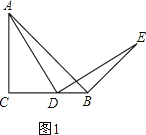
（1）如图1，点D在BC边上．

①依题意补全图1；

②作DF⊥BC交AB于点F，若AC=8，DF=3，求BE的长；

（2）如图2，点D在BC边的延长线上，用等式表示线段AB、BD、BE之间的数量关系（直接写出结论）．

Answer 1

【答案】（1）①图见解析；②BE=5；（2）见解析.

【解析】

（1）①根据题意画出图形即可；

②根据SAS证明△ADF≌△EDB，根据全等三角形的性质得到AF=EB．在△ABC和△DFB中，根据勾股定理得到AB=8，BF=3．再根据线段的和差关系得到AF=AB-BF=5，即BE=5．

（2）根据AAS证明△ACD≌△DFE，根据全等三角形的性质得到EF=DC．再根据等腰直角三角形的性质得到EF=BE，BC=AB，根据等量关系即可得到BD=BE+AB．

（1）①补全图形，如图1所示．

②如图1②，

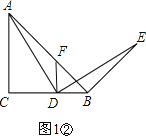
由题意可知AD=DE，∠ADE=90°．

∵DF⊥BC，

∴∠FDB=90°．

∴∠ADF=∠EDB．

∵∠C=90°，AC=BC，

∴∠ABC=∠DFB=45°．

∴DB=DF．

∴△ADF≌△EDB．

∴AF=EB．

在△ABC和△DFB中，

∵AC=8，DF=3，

∴A=8，BF=3．

AF=AB-BF=5

即BE=5．

（2）如图2，

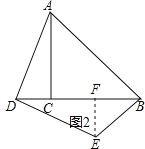
BD=BE+AB．