题目内容
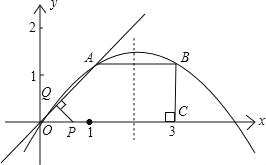
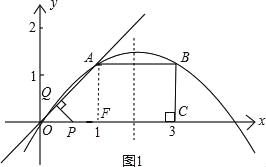
【题目】如图所示,已知在直角梯形OABC中,AB∥OC,BC⊥x轴于点C、A(1,1)、B(3,1).动点P从O点出发,沿x轴正方向以每秒1个单位长度的速度移动.过P点作PQ垂直于直线OA,垂足为Q.设P点移动的时间为t秒(0<t<4),△OPQ与直角梯形OABC重叠部分的面积为S.
(1)求经过O、A、B三点的抛物线解析式;
(2)求S与t的函数关系式;
(3)将△OPQ绕着点P顺时针旋转90°,是否存在t,使得△OPQ的顶点O或Q在抛物线上?若存在,直接写出t的值;若不存在,请说明理由.
【答案】(1)y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() ;(2)S=
;(2)S=![]() t2(0<t≤2);S=t-1(2<t≤3);S=﹣
t2(0<t≤2);S=t-1(2<t≤3);S=﹣![]() t2+4t﹣
t2+4t﹣![]() (3<t<4);(3)存在;t=1或2;
(3<t<4);(3)存在;t=1或2;
【解析】
(1)设出此抛物线的解析式,把A、B两点的坐标代入此解析式求出a、b的值即可;
(2)由与t的取值范围不能确定,故应分三种情况进行讨论,
①当0<t≤2,重叠部分的面积是S△OPQ,过点A作AF⊥x轴于点F,在Rt△OPQ中利用三角形的面积公式及特殊角的三角函数值即可求出其面积;
②当2<t≤3,设PQ交AB于点G,作GH⊥x轴于点H,∠OPQ=∠QOP=45°,则四边形OAGP是等腰梯形,
重叠部分的面积是S梯形OAGP,由梯形的面积公式即可求解;
③当3<t<4,设PQ与AB交于点M,交BC于点N,重叠部分的面积是S五边形OAMNC.
因为△PNC和△BMN都是等腰直角三角形,所以重叠部分的面积是S五边形OAMNC=S梯形OABC-S△BMN,进而可求出答案;
(3)根据图形旋转的性质可求出将△OPQ绕着点P顺时针旋转90°时P、Q两点的坐标,再根据抛物线的解析式即可求出t的值.
(1)方法一:由图象可知:抛物线经过原点,
设抛物线解析式为y=ax2+bx(a≠0).
把A(1,1),B(3,1)代入上式得:
![]() ,
,
解得![]() .
.
∴所求抛物线解析式为y=﹣![]() x2+
x2+![]() x.
x.
方法二:∵A(1,1),B(3,1),
∴抛物线的对称轴是直线x=2.
设抛物线解析式为y=a(x﹣2)2+h(a≠0)
把O(0,0),A(1,1)代入
得![]() ,
,
解得![]() ,
,
∴所求抛物线解析式为y=﹣![]() (x﹣2)2+
(x﹣2)2+![]() .
.
(2)分三种情况:
①当0<t≤2,重叠部分的面积是S△OPQ,过点A作AF⊥x轴于点F,
∵A(1,1),
∴在Rt△OAF中,AF=OF=1,∠AOF=45°,在Rt△OPQ中,OP=t,∠OPQ=∠QOP=45°,
∴PQ=OQ=tcos 45°=![]() t.S=
t.S=![]() t2,
t2,
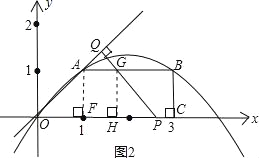
②当2<t≤3,设PQ交AB于点G,作GH⊥x轴于点H,∠OPQ=∠QOP=45°,
则四边形OAGP是等腰梯形,重叠部分的面积是S梯形OAGP.
∴AG=FH=t﹣2,
∴S=![]() (AG+OP)AF=
(AG+OP)AF=![]() (t+t﹣2)×1=t﹣1.
(t+t﹣2)×1=t﹣1.
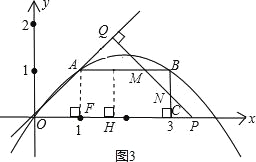
③当3<t<4,设PQ与AB交于点M,交BC于点N,重叠部分的面积是S五边形OAMNC.
因为△PNC和△BMN都是等腰直角三角形,
所以重叠部分的面积是S五边形OAMNC=S梯形OABC﹣S△BMN.
∵B(3,1),OP=t,
∴PC=CN=t﹣3,
∴S=![]() (2+3)×1﹣
(2+3)×1﹣![]() (4﹣t)2,
(4﹣t)2,
S=﹣![]() t2+4t﹣
t2+4t﹣![]() .
.
(3)存在.
当O点在抛物线上时,将O(t,t)代入抛物线解析式,解得t=0(舍去),t=1;
当Q点在抛物线上时,Q(![]() t,
t,![]() t)代入抛物线解析式得t=0(舍去),t=2.
t)代入抛物线解析式得t=0(舍去),t=2.
故t=1或2.
 .
.

【题目】某市团委举办“我的中国梦”为主题的知识竞赛,甲、乙两所学校参赛人数相等,比赛结束后,发现学生成绩分别为70分、80分、90分、100分,并根据统计数据绘制了如下不完整的统计图表:

乙校成绩统计表
分数/分 | 人数/人 |
70 | 7 |
80 | |
90 | 1 |
100 | 8 |
(1)在图①中,“80分”所在扇形的圆心角度数为________;
(2)请你将图②补充完整;
(3)求乙校成绩的平均分;
(4)经计算知s甲2=135,s乙2=175,请你根据这两个数据,对甲、乙两校成绩作出合理评价.