题目内容
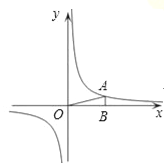
【题目】如图,在直角坐标系中,O为坐标原点.已知反比例函数y=![]() (k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为
(k>0)的图象经过点A(2,m),过点A作AB⊥x轴于点B,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)点C(x,y)在反比例函数y=![]() 的图象上,求当1≤x≤3时函数值y的取值范围;
的图象上,求当1≤x≤3时函数值y的取值范围;
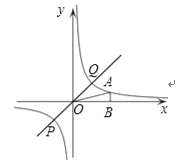
(3)过原点O的直线l与反比例函数y=![]() 的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
的图象交于P、Q两点,试根据图象直接写出线段PQ长度的最小值.
【答案】(1)m=![]() k=1(2)
k=1(2)![]() ≤y≤1(3)2
≤y≤1(3)2![]()
【解析】试题分析:(1)根据三角形的面积公式先得到m的值,然后把点A的坐标代入y=![]() ,可求出k的值;
,可求出k的值;
(2)根据反比例函数得性质求解;
(3)P,Q关于原点对称,则PQ=2OP,设P(a,![]() ),根据勾股定理得到OP=
),根据勾股定理得到OP=![]() ,从而得到OP最小值为
,从而得到OP最小值为![]() ,于是可得到线段PQ长度的最小值.
,于是可得到线段PQ长度的最小值.
试题解析:(1)∵A(2,m),
∴OB=2,AB=m,
∴S△AOB=![]() OBAB=
OBAB=![]() ×2×m=
×2×m=![]() ,
,
∴m=![]() ;
;
∴点A的坐标为(2,![]() ),
),
把A(2,![]() )代入y=
)代入y=![]() ,得
,得![]() ,
,
∴k=1;
(2)∵当x=1时,y=1;当x=3时,y=![]() ,
,
又∵反比例函数y=![]() ,在x>0时,y随x的增大而减小,
,在x>0时,y随x的增大而减小,
∴当1≤x≤3时,y的取值范围为![]() ≤y≤1;
≤y≤1;
(3)由图象可得:P,Q关于原点对称,
∴PQ=2OP,
反比例函数解析式为y=![]() ,设P(a,
,设P(a,![]() ),
),
∴OP=![]() ,
,
∴OP最小值为![]() ,
,
∴线段PQ长度的最小值为2![]() .
.

练习册系列答案
 优生乐园系列答案
优生乐园系列答案
相关题目