题目内容
【题目】在平面直角坐标系xOy中,过⊙C上一点P作⊙C的切线l.当入射光线照射在点P处时,产生反射,且满足:反射光线与切线l的夹角和入射光线与切线l的夹角相等,点P称为反射点.规定:光线不能“穿过”⊙C,即当入射光线在⊙C外时,只在圆外进行反射;当入射光线在⊙C内时,只在圆内进行反射.特别地,圆的切线不能作为入射光线和反射光线.
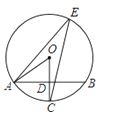
光线在⊙C外反射的示意图如图1所示,其中∠1=∠2.
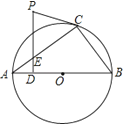
(1)自⊙C内一点出发的入射光线经⊙C第一次反射后的示意图如图2所示,P1是第1个反射点.请在图2中作出光线经⊙C第二次反射后的反射光线;
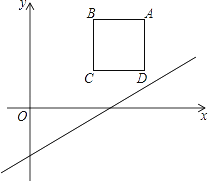
(2)当⊙O的半径为1时,如图3,
①第一象限内的一条入射光线平行于x轴,且自⊙O的外部照射在其上点P处,此光线经⊙O反射后,反射光线与y轴平行,则反射光线与切线l的夹角为;
②自点A(﹣1,0)出发的入射光线,在⊙O内不断地反射.若第1个反射点P1在第二象限,且第12个反射点P12与点A重合,则第1个反射点P1的坐标为
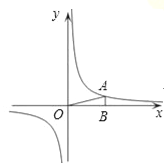
(3)如图4,点M的坐标为(0,2),⊙M的半径为1.第一象限内自点O出发的入射光线经⊙M反射后,反射光线与坐标轴无公共点,求反射点P的纵坐标的取值范围.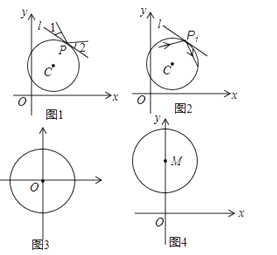
【答案】解:(1)答案如图: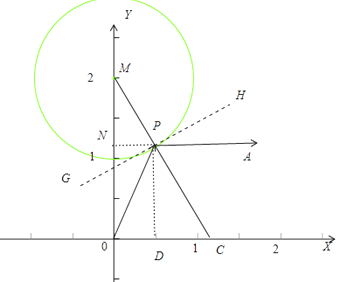
(2)
①由题意:∠1=∠2,∠APB=90°,
∴∠1=45°,
∴反射光与切线的夹角为45°.
②由题意:这些反射点组成的多边形是正十二边形,
∴入射光线与反射光线夹角为150°,
∴∠AOP1=30°,∵OP1=1,
∴P1(﹣![]() ,
,![]() ).
).
(3)如图:
当反射光PA∥X轴时,反射光线与坐标轴没有交点.
作PD⊥OC,PN⊥OM垂足分别为M,N,设PD=m.
∵∠GPO=∠HPA,∠GPC=∠HPC=90°,
∴∠OPC=∠APC=∠PCO,∴OP=OC,
在RT△PON中,∵ON=PD=m,PN2=1﹣(2﹣m)2 ,
∴PO2=m2+1﹣(2﹣m)2 ,
∵PD∥OM,∵![]() ,∴CP=
,∴CP=![]() ,
,
CD2=(![]() )2﹣m2 ,
)2﹣m2 ,
∴OC=ON+CD,
OC2=(![]() +
+![]() )2 ,
)2 ,
由:PO2=OC2得到:(![]() )2﹣m2=(
)2﹣m2=(![]() +
+![]() )2 ,
)2 ,
∴m1=2﹣![]() ,(m2=2+
,(m2=2+![]() ,m3=4,不合题意舍弃),
,m3=4,不合题意舍弃),
∴根据左右对称性得到:满足条件的反射点P的纵坐标:1![]() .
.
【解析】(1)(2)两个问题,要根据题意,画出图象,可以解决.
(3)当反射光线平行X轴时,反射光线与坐标轴没有交点,只要求出这样的反射点,就可以解决这个问题了.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案