题目内容
【题目】从图![]() 所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
所示的风筝中可以抽象出几何图形,我们把这种几何图形叫做“筝形”.
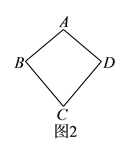
具体定义如下:如图![]() ,在四边形
,在四边形![]() 中,
中, ![]() ,
, ![]() ,我们把这种两组邻边分别相等的四边形叫做“筝形”.
,我们把这种两组邻边分别相等的四边形叫做“筝形”.

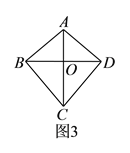
(![]() )结合图
)结合图![]() ,通过观察、测量、折纸,可以猜想“筝形”具有诸如“
,通过观察、测量、折纸,可以猜想“筝形”具有诸如“![]() 平分
平分![]() 和
和![]() ”这样的性质,请结合图形,再写出两条“筝形”的性质.
”这样的性质,请结合图形,再写出两条“筝形”的性质.
①____________________________.
②____________________________.
(![]() )从你写出的两条性质中,任选一条“筝形”的性质给出证明.
)从你写出的两条性质中,任选一条“筝形”的性质给出证明.
【答案】(![]() )①
)①![]() .②
.②![]() ,
, ![]() .(
.(![]() )见解析
)见解析
【解析】试题分析:(1)①一组对角相等,∠ABC=∠ADC;②AC垂直平分BD,OB=OD,BD⊥AC;(2)证明∠ABC=∠ADC,由已知条件不难证明△ABC≌△ADC,即可证明∠ABC=∠ADC.
试题解析:
(1)①一组对角相等,∠ABC=∠ADC;
②AC垂直平分BD,OB=OD,BD⊥AC.
(2)证明:∠ABC=∠ADC,
证:在△ABC和△ADC中,
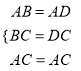 ,
,
∴△ABC≌△ADC(SSS),
∴∠ABC=∠ADC.

练习册系列答案
相关题目


