Question

【题目】如图，△ABC中，点E、P在边AB上，且AE=BP，过点E、P作BC的平行线，分别交AC于点F、Q，记△AEF的面积为S1 ， 四边形EFQP的面积为S2 ， 四边形PQCB的面积为S3 ．

（1）求证：EF+PQ=BC；
（2）若S1+S3=S2 ， 求的值；
（3）若S3﹣S1=S2 ， 直接写出的值．

Answer 1

【答案】
（1）

证明：∵EF∥BC，PQ∥BC，

∴，，

∵AE=BP，

∴AP=BE，

∴==1，

∴=1，

∴EF+PQ=BC；

（2）

解：过点A作AH⊥BC于H，分别交PQ于M、N，如图所示：

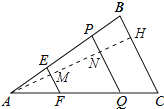
设EF=a，PQ=b，AM=h，

则BC=a+b，

∵EF∥PQ，

∴△AEF∽△APQ，

∴=，

∴AN=，MN=（﹣1）h，

∴S1=ah，S2=（a+b）（﹣1）h，S3=（b+a+b）h，

∵S1+S3=S2，

∴ah+（a+b+b）h=（a+b）（﹣1）h，

解得：b=3a，

∴=3，

∴=2；

（3）

解：∵S3﹣S1=S2，

∴（a+b+b）h﹣ah=（a+b）（﹣1）h，

解得：b=（1±）a（负值舍去），

∴b=（1+）a，

∴=1+，

∴=．

【解析】（1）由平行线得出比例式，，证出AP=BE，得出=1，即可得出EF+PQ=BC；
（2）过点A作AH⊥BC于H，分别交PQ于M、N，设EF=a，PQ=b，AM=h，则BC=a+b，由平行线得出△AEF∽△APQ，得出=，得出AN=，MN=（﹣1）h，
由三角形的面积公式得出S1=ah，S2=（a+b）（﹣1）h，S3=（b+a+b）h，得出ah+（a+b+b）h=（a+b）（﹣1）h，求出b=3a，即可得出结果；（3）由题意得出（a+b+b）h﹣ah=（a+b）（﹣1）h，得出b=（1+）a，即可得出结果．