题目内容
【题目】已知A（1，0）、B（0，-1）、C（-1，2）、D（2，-1）、E（4，2）五个点，抛物线y=a（x-1）2+k（a＞0）经过其中的三个点．
（1）求证：C、E两点不可能同时在抛物线y=a（x-1）2+k（a＞0）上；
（2）点A在抛物线y=a（x-1）2+k（a＞0）上吗？为什么？
（3）求a和k的值．
【答案】
（1）
解：∵抛物线y=a（x-1）2+k的对称轴为x=1，
而C（-1，2），E（4，2）两点纵坐标相等，
由抛物线的对称性可知，C、E关于直线x=1对称，
又∵C（-1，2）与对称轴相距2，E（4，2）与对称轴相距3，
∴C、E两点不可能同时在抛物线上；
（2）
解：假设点A（1，0）在抛物线y=a（x-1）2+k（a＞0）上，
则a（1-1）2+k=0，解得k=0，
因为抛物线经过5个点中的三个点，
将B（0，-1）、C（-1，2）、D（2，-1）、E（4，2）代入，
得出a的值分别为a=-1，a= 
，a=-1，a= 
，
所以抛物线经过的点是B，D，
又因为a＞0，与a=-1矛盾，
所以假设不成立．
所以A不在抛物线上；
而k为任意数，这与抛物线是确定的矛盾，故点A不在抛物线y=a（x-1）2+k（a＞0）上．
∴A点不在抛物线上
（3）
解：将D（2，-1）、C（-1，2）两点坐标代入y=a（x-1）2+k中，得
解得
或将E、D两点坐标代入y=a（x-1）2+k中，得 |
解得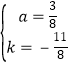
综上所述，
或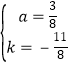
【解析】本题考查了二次函数图象上点的坐标特点．关键是明确图象上点的坐标必须满足函数解析式．（1）由抛物线y=a（x-1）2+k可知，抛物线对称轴为x=1，而C（-1，2），E（4，2）两点纵坐标相等，应该关于直线x=1对称，但C（-1，2）与对称轴相距2，E（4，2）与对称轴相距3，故不可能；（2）假设A点在抛物线上，得出矛盾排除A点在抛物线上；（3）B、D两点关于对称轴x=1对称，一定在抛物线上，另外一点可能是C点或E点，分别将C、D或D、E两点坐标代入求a和k的值．
