题目内容
【题目】在平面直角坐标系中,抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
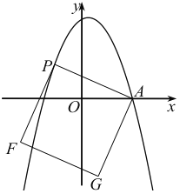
(1)求抛物线的解析式;
(2)![]() 为抛物线上的一个动点,点
为抛物线上的一个动点,点![]() 关于原点的对称点为
关于原点的对称点为![]() .当点
.当点![]() 落在该抛物线上时,求
落在该抛物线上时,求![]() 的值;
的值;
(3)![]()
![]() 是抛物线上一动点,连接
是抛物线上一动点,连接![]() ,以
,以![]() 为边作图示一侧的正方形
为边作图示一侧的正方形![]() ,随着点
,随着点![]() 的运动,正方形的大小与位置也随之改变,当顶点
的运动,正方形的大小与位置也随之改变,当顶点![]() 或
或![]() 恰好落在
恰好落在![]() 轴上时,求对应的
轴上时,求对应的![]() 点坐标.
点坐标.
【答案】(1)![]() .(2)
.(2)![]() 或
或![]() .(3)
.(3)![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,
 ,
,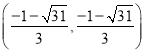 .
.
【解析】
(1)将![]() 和点
和点![]() 代入解析式解方程即可;
代入解析式解方程即可;
(2)将![]() 的坐标表示,把
的坐标表示,把![]() 坐标代入解析式求m即可;
坐标代入解析式求m即可;
(3)利用正方形性质和一线三直角几何模型,找到全等三角形,根据直角边解方程即可.
(1)∵抛物线![]() 经过点
经过点![]() 和点
和点![]() .
.
得![]() ,解得
,解得
∴抛物线的解析式为![]() .
.
(2)∵![]() 与
与![]() 关于原点对称,
关于原点对称,
∴![]() 的坐标为
的坐标为![]() .
.
∵![]() ,
,![]() 都在抛物线
都在抛物线![]() 上,
上,
∴![]() ,
,![]() .
.
∴![]() .
.
解得![]() 或
或![]() .
.
(3)当点![]() 落在
落在![]() 轴上时,
轴上时,
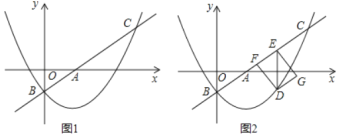
如图1,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
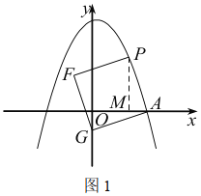
∵四边形![]() 是正方形,
是正方形,
∴![]() ,
,![]() .
.
∴![]() .
.
∵![]() ,
,
∴![]() .
.
∴![]() .
.
又![]() ,
,
∴![]() .
.
∴![]() .
.
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 点坐标为
点坐标为![]() .
.
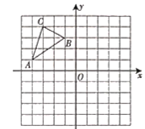
如图2,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,

同理可以证得![]() ,
,
∴![]() .
.
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 点坐标为
点坐标为![]() .
.
当点![]() 落在
落在![]() 轴上时,
轴上时,
如图3,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,

同理可以证得![]() ,
,
∴![]() ,
,
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 点坐标为
点坐标为 .
.
如图4,过点![]() 作
作![]() 轴于点
轴于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,

同理可以证得![]() ,
,
∴![]() ,
,
∴![]() ,有
,有![]() ,
,
解得![]() 或
或![]() (舍去).
(舍去).
∴![]() 点坐标为
点坐标为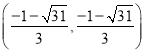 .
.
综上所述,![]() 点的坐标为
点的坐标为![]() ,
,![]() ,
,
 ,
,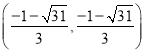 .
.

练习册系列答案
 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案
相关题目