题目内容
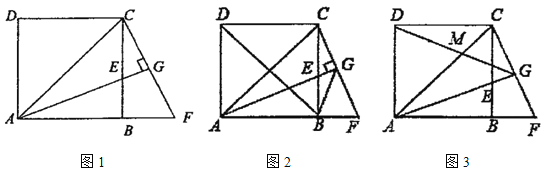
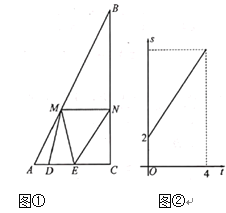
【题目】如图①,![]() 中,
中,![]() ,点
,点![]() 从点
从点![]() 出发沿
出发沿![]() 方向匀速运动,速度为1
方向匀速运动,速度为1![]() 点
点![]() 是
是![]() 上位于点
上位于点![]() 右侧的动点,点
右侧的动点,点![]() 是
是![]() 上的动点,在运动过程中始终保持
上的动点,在运动过程中始终保持![]() ,
,![]() cm.过
cm.过![]() 作
作![]() 交
交![]() 于
于![]() ,当点
,当点![]() 与点
与点![]() 重合时点
重合时点![]() 停止运动.设
停止运动.设![]() 的而积为
的而积为![]() ,点
,点![]() 的运动时问为
的运动时问为![]() ,
,![]() 与
与![]() 的函数关系如图②所示:
的函数关系如图②所示:
(1)![]() =_______
=_______![]() ,
,![]() =_______
=_______![]() ;
;
(2)设四边形![]() 的面积为
的面积为![]() ,求
,求![]() 的最大值;
的最大值;
(3)是否存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?如果存在,求
相似?如果存在,求![]() 的值;如果不存在,说明理由.
的值;如果不存在,说明理由.
【答案】(1)6,12;(2)![]() 时,
时,![]() 有最大值16.(3)
有最大值16.(3)![]() 或
或![]()
【解析】
(1)当t=4时,点E与C重合,此时AD=4,AC=AD+DE=4+2=6,故可求得AC=6;
由图分析当t=0时,S![]() =2.设M到AC的距离为h,所以
=2.设M到AC的距离为h,所以![]() DE
DE![]() h=2,所以h=2.易求得tan∠A=2,再在Rt
h=2,所以h=2.易求得tan∠A=2,再在Rt![]() 中,解直角三角形可以求出AC的长.
中,解直角三角形可以求出AC的长.
(2) 四边形![]() 的面积等于三角形MDE和三角形MNE的和,用含有t的式子表示出四边形MDEN的面积,再求最值;
的面积等于三角形MDE和三角形MNE的和,用含有t的式子表示出四边形MDEN的面积,再求最值;
(3)两个三角形中已有![]() ,如若再找到一对角相等,两三角形相似,故需分情况进行讨论:当
,如若再找到一对角相等,两三角形相似,故需分情况进行讨论:当![]() 或
或![]() 时,两三角形相似.
时,两三角形相似.
解:(1)由图可知:当t=4时,点E与C重合,此时AD=4,AC=AD+DE=4+2=6,故可求得AC=6;
当t=0时,S![]() =2.设M到AC的距离为h,所以
=2.设M到AC的距离为h,所以![]() DE
DE![]() h=2,所以h=2.
h=2,所以h=2.
∴tan∠A=![]() =2.
=2.
在Rt![]() 中,tan∠A=
中,tan∠A=![]() =2.
=2.
∴BC=2AC=12.
(2)作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,
,
又∴![]() ,
,
∴![]() ,
,
∴四边形![]() 是矩形,
是矩形,
∴![]() ,
,
∴![]()
![]() ,
,
根据题意,![]() ,
,
∴![]() 时,
时,![]() 有最大值16.
有最大值16.
(3)假设存在![]() 的值,使得以
的值,使得以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.
∵![]() ,∴
,∴![]() .
.
①当![]() 时,
时,![]() ,∴
,∴![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
②当![]() 时,
时,![]() ,此时
,此时![]() ,
,
∵![]() ,∴
,∴![]() ,∴
,∴![]() ,
,
∴![]() ,
,![]() (舍去)
(舍去)
∴![]() 或
或![]() 时,以
时,以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似.
相似.

练习册系列答案
 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案
相关题目