题目内容
【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,⊙O为△ABC 的内切圆,点D是斜边AB的中点,则tan∠ODA=_______.

【答案】2
【解析】试题分析:连接OE,OF,OG;
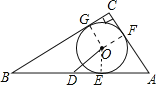
∵∠C=90°,AC=6,BC=8,
∴AB=10,
∵⊙O为△ABC的内切圆,
∴OG⊥BC,OF⊥AC,OE⊥AB,AF=AE,CF=CG,
∴∠OGC=∠OFC=∠OED=90°;
∵∠C=90°,
∴四边形OFCG是矩形,
∵OG=OF,
∴四边形OFCG是正方形;
设OF=x,则CF=CG=OF=x,AF=AE=6-x,BE=BG=8-x,
∴6-x+8-x=10,解得x=2,
∴OF=2,
∴AE=AF=AC-CF=4;
∵点D是斜边AB的中点,
∴AD=![]() AB=5,
AB=5,
∴DE=AD-AE=1,
∴tan∠ODA=![]() =2.
=2.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目