题目内容
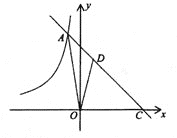
【题目】如图，⊙O的半径为2，点C是圆上的一个动点，CA⊥x轴，CB⊥y轴，垂足分别为A、B，D是AB的中点，如果点C在圆上运动一周，那么点D运动过的路程长为（ ）
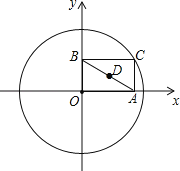
A.
B.
C.πD.2π
【答案】D
【解析】
根据题意可知，四边形OACB是矩形，D为AB的中点，连接OC，可知D点是矩形的对角线的交点，那么当C点绕圆O旋转一周时，D点也会以OD长为半径旋转一周，D点的轨迹是一个以O为圆心，以OD长为半径的圆，计算圆的周长即可.
如图，连接OC，
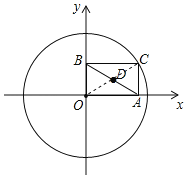
∵CA⊥x轴，CB⊥y轴，
∴四边形OACB是矩形，
∵D为AB中点，
∴点D在AC上，且OD＝
OC，
∵⊙O的半径为2，
∴如果点C在圆上运动一周，那么点D运动轨迹是一个半径为1圆，
∴点D运动过的路程长为2π1＝2π，
故选：D．
练习册系列答案
相关题目
