题目内容
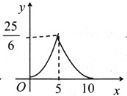
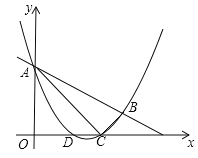
【题目】如图,在平面直角坐标系![]() 中,函数
中,函数![]() 的图象与函数
的图象与函数![]() 的图象相交于点A,并与
的图象相交于点A,并与![]() 轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
轴交于点C,S△AOC=15.点D是线段AC上一点,CD:AC=2:3.
(1)求![]() 的值;
的值;
(2)求点D的坐标;
(3)根据图象,直接写出当![]() 时不等式
时不等式![]() 的
的![]() 的解集.
的解集.
【答案】(1)-6;(2)D(1,4);(3)![]()
【解析】
(1)令y=0,则-x+5=0,解得x=5,即OC=5;然后根据S△AOC=15,可得yA=6,将![]() 代入
代入![]() 得
得![]() ,则A点坐标为(-1,6),最后代入
,则A点坐标为(-1,6),最后代入![]() ,即可确定k的值;
,即可确定k的值;
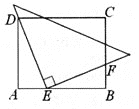
(2)作![]() 轴于E,作
轴于E,作![]() 轴于F,则
轴于F,则![]() ,然后再根据相似三角形的判定和性质解答,求出
,然后再根据相似三角形的判定和性质解答,求出![]() ,
,![]() ,最后将x=-1代入即可求解;
,最后将x=-1代入即可求解;
(3)根据函数图像进行解答即可.
解:(1)令y=0,
则-x+5=0,
∴x=5,
∴![]() ,
,![]() ,
,
![]() ,
,
∴![]() ,
,
把![]() 代入y=-x+5得,x=-1,
代入y=-x+5得,x=-1,
∴![]() ,
,
∵![]() 在函数
在函数![]() 的图象上,
的图象上,
∴![]() ;
;
(2)作![]() 轴于E,作
轴于E,作![]() 轴于F,则
轴于F,则![]() ,
,
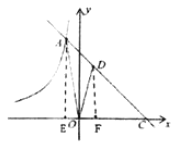
∵AE//DF,
∴CD:AC=CF:CE=2:3,
∴CF=4,
∴EF=2,OF=1,
把x=1代入y=-x+5得y=4,
∴![]() ;
;
(3)由图像得,当x<0时不等式![]() 的
的![]() 的解集为
的解集为![]()

练习册系列答案
相关题目