题目内容
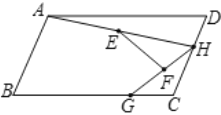
【题目】如图,在![]() 中,点
中,点![]() 是
是![]() 的中点,点
的中点,点![]() 是线段
是线段![]() 的延长线上的一动点,连接
的延长线上的一动点,连接![]() ,过点
,过点![]() 作
作![]() 的平行线
的平行线![]() ,与线段
,与线段![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.

![]() 求证:四边形
求证:四边形![]() 是平行四边形.
是平行四边形.
![]() 若
若![]() ,
,![]() ,则在点
,则在点![]() 的运动过程中:
的运动过程中:
①当![]() ________时,四边形
________时,四边形![]() 是矩形,试说明理由;
是矩形,试说明理由;
②当![]() ________时,四边形
________时,四边形![]() 是菱形.
是菱形.
【答案】(1)、证明过程见解析;(2)、①、2;②、4.
【解析】
(1)、首先证明△BEF和△DCF全等,从而得出DC=BE,结合DC和AB平行得出平行四边形;(2)、①、根据矩形得出∠CEB=90°,结合∠ABC=120°得出∠CBE=60°,根据直角三角形的性质得出答案;②、根据菱形的性质以及∠ABC=120°得出△CBE是等边三角形,从而得出答案.
(1)、证明:∵AB∥CD,∴∠CDF=∠FEB,∠DCF=∠EBF,∵点F是BC的中点,
∴BF=CF,在△DCF和△EBF中,∠CDF=∠FEB,∠DCF=∠EBF,FC=BF,
∴△EBF≌△DCF(AAS), ∴DC=BE, ∴四边形BECD是平行四边形;
(2)、①BE=2;∵当四边形BECD是矩形时,∠CEB=90°,∵∠ABC=120°,∴∠CBE=60°;
∴∠ECB=30°,∴BE=![]() BC=2,
BC=2,
②BE=4,∵四边形BECD是菱形时,BE=EC,∵∠ABC=120°,∴∠CBE=60°,
∴△CBE是等边三角形,∴BE=BC=4.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目