题目内容
【题目】观察下列数表
根据数表反映的规律，猜想第6行与第6列的交叉点上的数应为多少．
（1）第n行与第n列的交叉点上的数应为多少．（用含正整数n的式子表示）
（2）计算左上角2×2的正方形里所有数字之和，即：
在数表中任取几个2×2的正方形，计算其中所有数字之和，归纳你得出的结论．
【答案】第（1）第6行与第6列的交叉点上的数是11，第n行与第n列的交叉点上的数应为（2n﹣1）；（2）四个数的和是n+（﹣n+1）+（﹣n+1）+（n﹣2）=0，结论：任取2×2的正方形上的四个数字的和都是0．
【解析】
观察所给四行可知，第1行与第1列的交叉点上的数是1，第2行与第2列的交叉点上的数是3=2×2﹣1，第3行与第3列的交叉点上的数是5=2×3﹣1，第4行与第4列的交叉点上的数是7=2×4﹣1，据此可求出，第6行与第6列的交叉点上的数；
（1）根据前面观察出的规律，可写出第n行与第n列的交叉点上的数；
（2）根据所得规律，表示出四个数相加即可求出结论.
第1行与第1列的交叉点上的数是1，
第2行与第2列的交叉点上的数是3=2×2﹣1，
第3行与第3列的交叉点上的数是5=2×3﹣1，
第4行与第4列的交叉点上的数是7=2×4﹣1，
所以，第6行与第6列的交叉点上的数是2×6﹣1=11；
（1）第n行与第n列的交叉点上的数应为（2n﹣1）；
（2）1+（﹣2）+（﹣2）+3=4+（﹣4）=0，
设2×2的正方形左上角的数是n（n＞0），则左下角的数是﹣（n+1），右上角的数是﹣（n+1），右下角的数是（n+2），
所以，四个数的和是n﹣（n+1）﹣（n+1）+（n+2）=2n+2﹣2n﹣2=0，
设2×2的正方形左上角的数是n（n＜0），则左下角的数是﹣n+1，右上角的数是﹣n+1，右下角的数是n﹣2，
所以，四个数的和是n+（﹣n+1）+（﹣n+1）+（n﹣2）=0，
结论：任取2×2的正方形上的四个数字的和都是0．
心算口算巧算一课一练系列答案
应用题作业本系列答案
【题目】为了解某地区七年级学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况，从该地区随机抽取部分七年级学生作为样本，采用问卷调查的方法收集数据（参与问卷调查的每名同学只能选择其中一类节目），并调查得到的数据用下面的表和扇形图来表示（表、图都没制作完成）
节目类型 | 新闻 | 体育 | 动画 | 娱乐 | 戏曲 |
人数 | 36 | 90 | a | b | 27 |
根据表、图提供的信息，解决以下问题：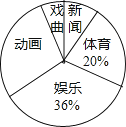
（1）计算出表中a、b的值；
（2）求扇形统计图中表示“动画”部分所对应的扇形的圆心角度数；
（3）若该地区七年级学生共有47500人，试估计该地区七年级学生中喜爱“新闻”类电视节目的学生有多少人？
